Funcţia de producţie şi utilizarea eficientă a resurselor
- Detalii
- Categorie: Microeconomie
- Accesări: 29,854
Pentru o inţelegere completă microeconomiei aplicate, este deosebit de important să cunoaştem teoria producţiei. Seria producţiei reprezintă fundamentul teoriei ofertei care, aşa cum aţi putut vedea, ne pune la dispoziţie conceptele esenţiale pentru a inţelege mecanismele de formare a preţurilor. Mai mult, deciziile de producţie joacă un rol determinant in procesul decizional.
Legat de producţie, managerii iau patru tipuri de decizii:
- dacă să continue producţia sau să o oprească;
- ce cantitate să producă;
- ce combinaţie de resurse să utilizeze;
- ce tehnologie să utilizeze.
Producţia presupune transformarea resurselor (capital, echipamente, muncă, pămant, informaţii) in produse sau servicii. In procesul de producţie, managerii sunt preocupaţi de eficienţa Utilizării resurselor. Pe baza obiectivelor legate de eficienţă, se stabilesc regulile de bază referitoare la modul in care organizaţiile trebuie să utilizeze resursele. Aceste obiective se impart in două categorii mari:
- minimizarea costurilor de realizare a unui anumit nivel de producţie;
- maximizarea producţiei realizate cu anumite costuri.
Funcţia de producţie
Funcţia de producţie reprezintă legătura dintre combinaţia de resurse utilizate şi nivelul producţiei posibil de realizat, utilizand un anumit tip de proces tehnologic.
Funcţia de producţie reprezintă un tabel, o funcţie sau un grafic, exprimand nivelul maxim de producţie care poate fi obţinut cu o anumită combinaţie de resurse, in condiţiile unui anumit proces tehnologic.
In producţie, se pot utiliza diferite resurse. De aceea, generalizand, putem spune că nivelul producţiei este in funcţie de cantităţile de resurse utilizate, adică:
Q = f(X1, X2, ..., X>n)
in care:
Q = nivelul producţiei
X1, X2, ..., Xn = totalitatea resurselor utilizate in procesul de producţie
Pentru a simplifica analiza, vom considera că un anumit produs poate fi realizat utilizand una sau două resurse, oprindu-ne la cele mai importante şi anume munca şi capitalul. Dorim să precizăm, insă, că aceleaşi principii se aplică şi in cazul utilizării unui număr mai mare de resurse.
Prin urmare:
Q = f (K,M)
in care:
K = consumul de capital
M = consumul de muncă
In cadrul proceselor de producţie, cat şi in cele de prestare a serviciilor, managerii trebuie să urmărească atat maximizarea eficienţei tehnice, cat şi a celei economice.
Eficienţa tehnică este atinsă atunci cand, cu o combinaţie de resurse dată, se realizează cantitatea maximă de producţie.
Eficienţa economică este atinsă atunci cand se realizează o anumită cantitate de producţie, cu un cost minim.
Un proces eficient din punct de vedere tehnic nu este neapărat eficient şi din punct de vedere economic. Să presupunem, de exemplu, că pierderile tehnologice de piele dintr-o fabrică de pantofi sunt prea mari. Pentru creşterea eficienţei tehnice, se poate face o modificare in cadrul procesului tehnologic, care să contribuie la reducerea substanţială a procentului de deşeuri. Pentru ca modificarea tehnologiei să fie insă eficientă şi din punct de vedere economic, investiţia necesară trebuie să fie mai mică decat costul deşeurilor de piele. Managerii trebuie să urmărească o reducere a costurilor totale.
Dacă preţul pielii este foarte mare, cantitatea consumată trebuie minimizată şi modificarea tehnologiei se justifică. Dacă, dimpotrivă, pielea este ieftină, iar modificarea procesului tehnologic presupune investiţii mari, se va păstra situaţia existentă. Prin urmare, din punct de vedere economic, eficienţa este stabilită in funcţie de preţul resurselor, astfel incat costul total al obţineriiunei anumite cantităţi de bunuri să fie minim. Atunci cand se analizează un anumit proces de producţie, este bine să se utilizeze clasificarea resurselor in fixe şi variabile.
Resursele fixe sunt acelea al căror nivel de utilizare nu poate fi schimbat intr-un interval scurt de timp.
Nici o resursă nu este absolut fixă, indiferent cat de scurt este intervalul de timp considerat. In orice caz, atunci cand modificările sunt nesemnificative şi costurile aferente acestor modificări sunt mici, ele sunt considerate fixe. In categoria resurselor fixe se includ clădirile, echipamentele mari, personalul managerial.
Resursele variabile sunt acelea al căror nivel de utilizare poate fi modificat intr-un interval scurt de timp, pentru a răspunde necesităţilor procesului de producţie.
In această categorie sunt incluse manopera, materiile prime şi semifabricatele. In funcţie de clasificarea de mai sus, economiştii fac distincţie intre termenul scurt şi termenul lung.
Producţia pe termen scurt
Termenul scurt reprezintă intervalul de timp (orizontul de planificare) in care una sau mai multe dintre resursele necesare in procesul de producţie sunt fixe, neputandu-se schimba cantitatea in care sunt utilizate. De aceea, pe termen scurt, modificările cantităţii de produse pot fi obţinute exclusiv prin schimbări in utilizarea resurselor variabile. Astfel, creşterea producţiei pe termen scurt se poate obţine prin mărirea timpului de lucru, a cantităţii de materii prime, in condiţiile in care se utilizează aceleaşi clădiri şi echipamente. Considerand capitalul ca fiind factor constant, funcţia de producţie pe termen scurt devine:
Q = f (K, M) = f (M)
in care: bararea lui K sugerează caracterul fix al capitalului.
Relaţia dintre producţia totală, productivitatea muncii şi produsul marginal
Să presupunem că in cazul unei anumite funcţii de producţie, se menţine constant nivelul capitalului, iar numărul de muncitori variază intre 0 şi 10. In tabelul 5.1 sunt prezentate următoarele date: numărul de muncitori, producţia totală, productivitatea muncii şi produsul marginal al muncii aferente fiecărui muncitor.
Tabelul 5.1 Relaţia dintre producţia totală, produsul marginal şi productivitatea muncii
| Numărul de muncitori | Producţia totală | Productivitatea muncii Q/M | Produsul marginal al muncii ΔQ/ΔM |
|---|---|---|---|
| 1 | 52 | 52 | 52 |
| 2 | 112 | 56 | 60 |
| 3 | 170 | 56,7 | 58 |
| 4 | 220 | 55 | 50 |
Productivitatea muncii, particularizare la situaţia forţei de muncă a noţiunii produs mediu al unei resurse, reprezintă raportul dintre producţia totală şi numărul de muncitori care contribuie la realizarea ei.
W = Q / M
in care:
W = productivitatea muncii.
Produsul marginal al muncii , particularizarea noţiunii produs marginal al unei resurse la situaţia forţei de muncă, reprezintă producţia suplimentară obţinută ca urmare a utilizării unui muncitor suplimentar, in condiţiile in care celelalte resurse sunt fixe.
PM = ΔQ / ΔM
in care:
PM = produsul marginal al muncii;
ΔQ = modificarea producţiei;
ΔM = modificarea numărului de muncitori.
După cum se poate observa din tabel, producţia creşte pană la al nouălea muncitor, după care scade. Evoluţia productivităţii muncii este prezentată in coloana a treia, iar cea a produsului marginal in oloana a patra a tabelului. Produsul marginal are o evoluţie normală: mai intai creşte, după care descreşte, devenind negativ la un moment dat.
Dorim să precizăm că se calculează produsul marginal al muncii şi nu produsul marginal al unui anumit muncitor. De exemplu, atunci cand creşte numărul de muncitori de la 7 la 8, se consideră că toţi muncitorii acţionează la fel, contribuind in măsură egală la creşterea producţiei de la 304 la 314 unităţi.
In figura 5.1 se reprezintă grafic relaţia dintre producţia totală, produsul marginal şi produsul mediu – in situaţia de faţă productivitatea muncii.
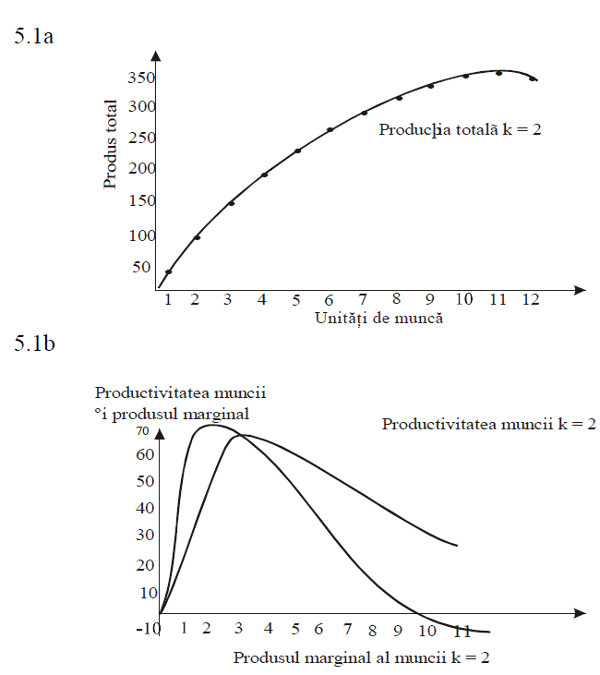
Figura 5.1 Relaţia dintre producţia totală, productivitatea muncii şi produsul marginal
In figura 5.1 a se poate observa cum producţia totală creşte continuu pană la 10 muncitori, in ritmuri diferite, mai intai crescătoare, apoi descrescătoare, după care incepe să scadă. Figura 5.1 b este reprezentarea unei evoluţii normale a produsului marginal şi a productivităţii muncii: produsul marginal al muncii creşte, pe intervalul in care producţia totală creşte in ritm crescător (0 muncitori – 2 muncitori), ajunge la maximum la 2 muncitori, după care scade, pe intervalul in care producţia totală creşte in ritm descrescător (2 muncitori – 10 muncitori), devenind negativ atunci cand producţia scade la 10 muncitori. Productivitatea muncii creşte pe intervalul 0 – 4 muncitori, unde atinge maximul, apoi scade. Atata timp cat productivitatea muncii creşte, este mai mică decat produsul marginal al muncii, cu excepţia primului muncitor, cand este egală cu acesta. Curba productivităţii muncii intersectează curba produsului marginal al muncii in punctul ei de maxim, la 3 muncitori. Apoi, productivitatea muncii scade, dar este superioară produsului marginal al muncii. Produsul marginal incepe deci să scadă inainte de productivitatea muncii.
Legea randamentului descrescător al muncii
Evoluţia curbei produsului marginal din figura 5.1 ilustrează o lege importantă a microeconomiei şi anume legea randamentului descrescător al muncii. In condiţiile in care toate celelalte resurse sunt constante, pe măsura creşterii cantităţii de resurse variabile, există un punct dincolo de care produsul marginal al resursei variabile respective scade. Cand cantitatea din resursa variabilă (in cazul nostru munca) este mică in comparaţie cu resursele fixe (de exemplu, utilaje tehnologice), creşterea cantităţii de resurse variabile utilizate conduce iniţial la creşterea produsului ei marginal.
Dincolo de un anumit punct, creşterea cantităţii din resursa respectivă va aduce insă un plus din ce in ce mai mic de producţie, pentru că fiecare unitate suplimentară de resursă variabilă are, in medie, un număr din ce in ce mai mic de resurse fixe cu care lucrează.
Prin urmare:
Legea randamentului descrescător al muncii arată că atunci cand resursele fixe (utilaje, clădiri, aparat managerial etc.) sunt menţinute constante, produsul marginal al muncii creşte la inceput, după care incepe să scadă, deoarece cantitatea de resurse fixe, care revine pe o unitate demuncă, este din ce in ce mai mică.
Deşi nu se demonstrează matematic, această lege, care stabileşte relaţia fizică dintre muncă şi capital, este o consecinţă a observaţiilor practice, care nu au fost niciodată contrazise. In figura 5.2, se redă o reprezentare simplificată, mai clară, a relaţiei dintre producţia totală, productivitatea muncii şi produsul marginal al muncii. Aşa cum am explicat şi pe baza figurii 5.1, din figura 5.2 rezultă următoarele tendinţe:
- la zero muncitori producţia este zero.
- pe intervalul 0 – M0, producţia creşte in ritm crescător de la 0 la Q0; pe acest interval produsul marginal creşte.
- pe intervalul M0 – M2, producţia creşte in ritm descrescător; pe acest interval, produsul marginal descreşte.
- incepand cu M2 producţia incepe să scadă, produsul marginal fiind negativ.
- produsul marginal incepe să descrească in punctul M0, inaintea productivităţii muncii, care incepe să scadă in punctul M1.
- productivitatea muncii, şi produsul marginal al muncii se intersectează in punctul M1, unde productivitatea muncii este maximă.
- după punctul de intersecţie, productivitatea muncii este mai mare decat produsul marginal al muncii.
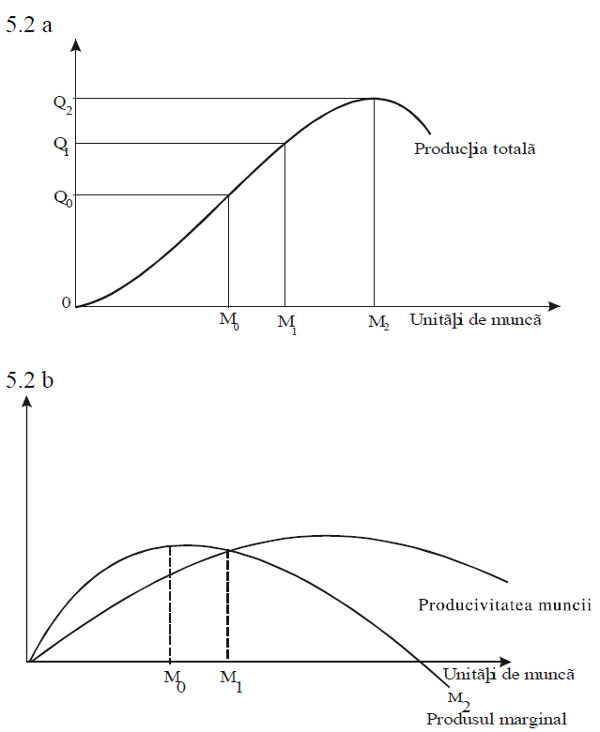
Figura 5.2 Curbele producţiei totale, produsului marginal şi productivităţii munci
Producţia pe termen lung
Termenul lung reprezintă intervalul de timp (orizontul de planificare) in care toate resursele ce se utilizează in procesul de producţie sunt variabile.
Prin urmare, pe termen lung toate resursele pot fi modificate din punct de vedere cantitativ şi calitativ, astfel incat procesul de producţie să fie eficient din punct de vedere tehnologic şi economic. De exemplu, pe termen lung, producţia poate fi suplimentată prin creşterea capacităţilor de producţie sau prin aducerea unor utilaje noi, mai performante.
Isocuantele producţiei
La fel cum am procedat şi in cadrul analizei funcţiei de producţie pe termen scurt, vom utiliza şi in analiza funcţiei de producţie pe termen lung doar combinaţii de două resurse, muncă şi capital, pentru a putea utilize reprezentările grafice. Principiile pe care le vom stabili sunt insă valabile şi pentru combinaţii de mai multe resurse. Instrumentul de analiză in situaţia in care cele două resurse utilizate variază este isocuanta.
Isocuanta este curba (mulţimea de puncte) care descrie totalitatea combinaţiilor de resurse cu ajutorul cărora se poate obţine un anumit nivel maxim al producţiei. Cu alte cuvinte, acelaşi nivel de producţie poate fi obţinut utilizand mai multă muncă şi mai puţin capital sau, invers, mai puţină muncă şi mai mult capital.
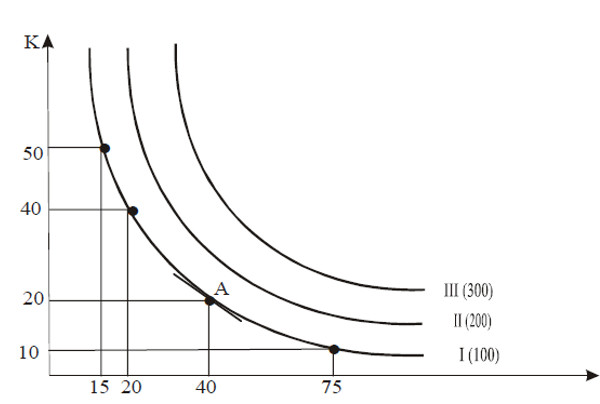
Figura 5.3 Isocuante
In figura 5.3 se prezintă trei isocuante. Isocuanta I prezintă toate combinaţiile de capital şi muncă cu ajutorul cărora se pot obţine 100 unităţi de producţie. Aşa cum reiese din figură, se pot obţine 100 unităţi de producţie cu 10 unităţi de capital şi 75 unităţi de muncă, cu 50 unităţi de capital şi 15 unităţi de muncă sau cu cu alte combinaţii. Similar, isocuanta II arată toate combinaţiile de capital şi muncă cu care se poate obţine o producţie de 200 de unităţi, iar izocuanta III pe cele pentru 300 de unităţi.Pot exista de fapt o infinitate de isocuante, pentru o infinitate de cantităţi de producţie. Isocuantele nu se intersectează niciodată.
Rata marginală de substituire tehnică
După cum se poate observa din figura 5.3, isocuantele au pantă negativă. Explicaţia constă in faptul că, pentru a se menţine producţia constantă, pe măsură ce se utilizează mai puţin capital, acesta trebuie inlocuit cu forţă de muncă. Invers, pentru a se menţine producţia constantă, pe măsură ce se utilizează mai puţină muncă, aceasta trebuie inlocuită cu capital. Deci, in scopul menţinerii producţiei constante, cele două tipuri de resurse se pot substitui reciproc.
Raportul in care poate fi substituită o resursă cu alta in scopul menţinerii constante a producţiei prezintă o importanţă teoretică deosebită şi se numeşte rata marginală de substituire tehnică.
Prin urmare:
Rata marginală de substituire tehnică reprezintă raportul in care o resursă (capitalul) este substituită cu o alta (munca de-a lungul isocuantei.
RMST = – (ΔK / ΔM)
in care:
ΔK = modificarea capitalului;
ΔM = modificarea cantităţii de muncă.
Panta isocuantei este negativă, deoarece renunţarea la o unitate de capital presupune utilizarea unui număr suplimentar de unităţi de muncă. Ca o consecinţă a randamentului descrescător al muncii, pe măsura creşterii consumului de muncă, pentru a substitui o unitate de capital la care se renunţă, va fi necesar un număr din ce in ce mai mare de unităţi de muncă.
Figura 5.3 demonstrează evoluţia descrescătoare a ratei marginale de substituire tehnică. Să studiem cazul isocuantei I, care descrie totalitatea combinaţiilor de muncă şi de capital cu ajutorul cărora se poate obţine o producţie de 100 unităţi. Putem observa că, atunci cand se reduce consumul de capital de la50 la 40 de unităţi, deci cu 10 unităţi, sunt necesare 5 unităţi suplimentare de muncă (20 in loc de 15), pentru menţinerea nivelului constant al producţiei la 100 unităţi. Deplasandu-ne spre zona inferioară a isocuantei, constatăm o creştere a numărului de unităţi suplimentare de muncă necesare pentru inlocuirea unei unităţi de capital la care se renunţă, astfel incat să se menţină producţia constantă.
Atunci cand se reduce numărul de unităţi de muncă, de data aceasta de la 20 la 10, consumul de muncă trebuie suplimentat cu 35 de unităţi (de la 40 la 75). Prin urmare, in primul caz, cand consumul de capital se reduce de la 50 la 40 unităţi, rata marginală de substituire tehnică este de – ΔK/ΔM = – (–10)/5 = 2, ceea ce inseamnă că in scopul fabricării unei producţii de 100 unităţi, atunci cand se utilizează o unitate suplimentară de muncă, se renunţă la utilizarea a 2 unităţi de capital. Dacă analizăm insă cazul in care cantitatea de capital se reduce de la 20 la 10 unităţi, deci tot cu 10 unităţi, pentru a crea 100 unităţi, cantitatea de muncă utilizată trebuie să crească cu 35 unităţi (de la 40 la 75). In acest caz, rata marginală de substituire tehnică este de 10/35, arătand că, la fiecare unitate de muncă adăugată, capitalul poate fi redus cu 0,28 unităţi.
Rezultă că, la deplasarea isocuantei, pe măsura utilizării unui număr mai mic de unităţi de capital, cantitatea de capital la care se poate renunţa in favoarea muncii scade. Sau, invers, cantitatea de muncă ce trebuie adăugată pentru a renunţa la o unitate de capital creşte.
Rata marginală de substituire tehnică, care are evoluţia prezentată mai sus, reprezintă de fapt panta isocuantei. Aşa se explică de ce isocuanta tinde asimptotic spre cele două axe. In cele ce urmează, vom explica o altă definiţie a ratei marginale de substituire tehnică, şi anume:
Rata marginală de substituire tehnică este egală cu raportul dintre produsul marginal al muncii şi produsul marginal al capitalului.
Nivelul producţiei depinde de modul de utilizare a celor două resurse, munca şi capitalul. Generalizand, putem spune că, la o mică variaţie a muncii şi capitalului, modificarea cantităţii de producţie rezultă din modificarea cantităţii celor două resurse, inmulţită cu produsul lor marginal:
ΔQ = PMMΔM + PMKΔK
ΔQ = modificarea producţiei;
PMM = produsul marginal al muncii;
PMK = produsul marginal al capitalului;
ΔM = modificarea cantităţii de muncă;
ΔK = modificarea cantităţii de capital.
Intrucat de-a lungul isocuantei producţia este constantă, inseamnă că indiferent cum vor evolua munca şi capitalul, variaţia cantităţii realizate este zero. Prin urmare, deoarece de-a lungul isocuantei:
ΔQ = 0
PMM ΔM + PMK ΔK = 0
De aici rezultă că:
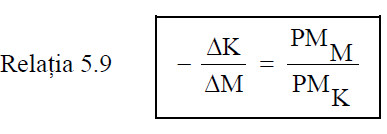
Să presupunem că intr-un anumit punct al isocuantei, produsul marginal al capitalului PMK este 3 şi produsul marginal al muncii PMM este 6. Deci, la creşterea cu o unitate a cantităţii de muncă, producţia va creşte cu 6 unităţi. Cantitatea de capital care trebuie scoasă din folosinţă pentru a menţine nivelul iniţial al producţiei Q trebuie să contracareze creşterea de producţie generată de munca suplimentară. Avand in vedere faptul că produsul marginal al capitalului este 3, vor trebui scoase din uz 2 unităţi de capital, care ar fi realizat cele 6 unităţi ce vor fi realizate prin suplimentarea muncii cu o unitate. In acest caz, rata marginală de substituire tehnică este RMST = -ΔK/ΔL = -(-2)/1 = 2, ceea ce este egal cu PMM/ PMk=6/3 = 2.
Or, la creşterea cu o unitate a capitalului, producţia va creşte cu 3 unităţi. In această situaţie rata marginală de substituire tehnică este RMST = -ΔK/ΔL = -(1) / (-1/2) = 2, ceea ce este din nou egal cu PMM/ PMk.
Această relaţie explică evoluţia descrescătoare a ratei marginale de substituire tehnică RMST, prin faptul că, pe măsura substituirii muncii cu capitalul, produsul marginal al muncii scade şi produsul marginal al capitalului creşte.
Combinaţia optimă de resurse
După cum am arătat anterior, o anumită cantitate de producţie poate fi obţinută utilizand mai multe combinaţii de resurse. Cand este posibilă substituirea unui tip de resursă cu un altul, in scopul obţinerii unei anumite cantităţi de producţie, se spune că resursele pot fi utilizate in proporţii variabile.
Producţia obţinută cu proporţii variabile de resurse este producţia care se poate realiza cu mai multe combinaţii de resurse.
In acest sens, managerii trebuie să determine, pe langă nivelul optim al producţiei, şi nivelul optim al combinaţiei de resurse cu care această producţie poate fi obţinută. Pe termen lung, pot fi modificate toate tipurile de resurse. Atunci cand fac o investiţie, managerii trebuie să aleagă dintre mai multe procese de producţie, astfel incat nivelul optim de producţie să se obţină cu o combinaţie optimă de resurse.
Producţia obţinută cu o proporţie fixă de resurse este producţia care, pentru a-şi menţine integral caracteristicile, trebuie realizată cu o singură combinaţie de resurse.
In cazul producţiei obţinute cu o proporţie fixă de resurse, extinderea sau reducerea producţiei este urmată de extinderea sau reducerea similară a fiecărui tip de resurse. Utilizarea unei proporţii fixe de resurse este valabilă numai pe termen scurt. Pe termen lung, o anumită cantitate de produse se poate obţine utilizand mai mult capital şi mai puţină forţă de muncă sau, dimpotrivă, mai puţin capital şi mai multă forţă de muncă. Utilizarea muncii şi a capitalului in proporţii diferite depinde de costul relativ al acestora, alegandu-se combinaţia cea mai eficientă din punct de vedere economic.
După cum a reieşit anterior, nivelul dorit al producţiei poate fi obţinut cu ajutorul a diferite combinaţii de resurse. Dar, aşa cum am precizat in introducerea acestui capitol, una dintre cele patru decizii pe care un manager trebuie să le ia o reprezintă alegerea combinaţiei optime de resurse. In funcţie de preţul resurselor, managerul are două posibilităţi:
- Să aleagă acea combinaţie de resurse cu ajutorul căreia se poate maximiza nivelul producţiei posibil a fi obţinută cu o cheltuială dată.
- Să aleagă acea combinaţie de resurse care minimizează cheltuiala cu care se poate obţine o anumită producţie.
Prin urmare:
Combinaţia optimă de resurse este acea combinaţie cu ajutorul căreia se poate obţine un anumit nivel de producţie cu costul minim sau un nivel maxim de producţie cu un cost dat.
Deci, organizaţia trebuie fie să-şi minimizeze costurile, pentru că are o restricţie legată de cantitatea de producţie pe care trebuie să o realizeze, fie să-şi maximizeze producţia, in funcţie de restricţia pe care o are relativ la costuri.
In continuare, vom utiliza metoda grafică pentru a vedea, pe de o parte, cum se pot minimiza costurile, atunci cand trebuie realizată o anumită producţie şi cum se poate maximiza producţia, pe de altă parte, atunci cand există constrangeri legate de costuri.
In reprezentarea grafică, vom utiliza principiile isocuantei, pe care le-am expus anterior. Este necesară, de asemenea, o metodă de includere in analiza grafică a preţului resurselor. Aceasta este utilizarea curbei isocost. De aceea, vom prezenta conceptul de curbe isocost şi relaţia lor cu preţul resurselor.
Preţul resurselor şi curbele isocost
Pentru a minimiza costurile necesare obţinerii unei anumite cantităţi de producţie sau pentru a maximiza cantitatea de producţie care poate fi obţinută cu anumite costuri, managerii trebuie să ia in considerare preţurile resurselor. Pentru producătorii care nu aparţin unei pieţe de monopol sau de oligopol (nu sunt singurul cumpărător sau unii dintre puţinii cumpărători de resurse de pe piaţă), preţul resurselor se stabileşte pe piaţa furnizorilor de resurse in funcţie de cerere şi de ofertă. Costul necesar pentru obţinerea unei anumite cantităţi de produse sau al unui anumit număr de servicii se calculează conform relaţiei:
C = aK + sM
in care:
C = costul total al realizării produselor sau serviciilor;
K = cantitatea necesară de capital;
M = cantitatea necesară de muncă ;
a = costul unitar al capitalului;
s = costul unitar al muncii.
Costul total este, deci, suma costului capitalului şi al costului muncii, in condiţiile unor costuri unitare date ale acestora.
Exemplu:
Să considerăm costul lunar al capitalului de 1.000.000 lei pe unitate (a = 1.000.000 lei), iar salariul lunar al unui muncitor de 2.500.000 lei (s = 2.500.000 lei). In aceste condiţii, funcţia costului total este:
C = 1.000.000K + 2.500.000M Să presupunem că managementul organizaţiei a decis să cheltuiască lunar 15.000.000 lei pentru resurse. In această situaţie, ecuaţia devine: 15.000.000 = 1.000.000K + 2.500.000M
Rezolvand ecuaţia, putem afla combinaţiile de capital şi de muncă ce pot fi alese. K = 15 – 2,5M Similar, in situaţia in care suma cheltuită pentru resurse este de 20.000.000 lei, relaţia dintre cele două resurse pe care va trebui să o adopte organizaţia este: K = 20 – 2,5M In situaţia in care organizaţia are la dispoziţie o sumă fixă pe care o poate cheltui pentru procurarea de resurse, ea poate să aleagă dintr-o mulţime de combinaţii, date de relaţia:
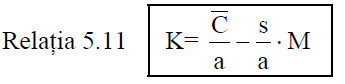
in care:
C = suma fixă pe care o poate cheltui organizaţia pentru procurarea de resurse;
K = cantitatea necesară de capital;
M = cantitatea necesară de muncă;
a = costul unitar al capitalului;
s = costul unitar al muncii.
Aceste ecuaţii sunt ilustrate in figura 5.4. Dacă se cheltuieşte o sumă de 15.000.000 lei pentru procurarea de resurse şi nu se atrage deloc muncă, pot fi procurate, conform relaţiei anterioare 15 unităţi de capital. Dacă se cheltuieşte o sumă de 20.000.000 lei pentru procurarea de resurse şi nu se atrage deloc muncă, pot fi procurate, conform relaţiei anterioare, 20 de unităţi de capital. Generalizand, dacă se va cheltui suma C şi „a” este costul unitar al capitalului, cantitatea maximă de capital care poate fi procurată va fi C/a unităţi. C/a este intersecţia isocostului cu ordonata.
La procurarea unei unităţi de muncă trebuie redus capitalul cu 2,5 unităţi. Dacă se suplimentează munca cu două unităţi, trebuie să se renunţe la 5 unităţi de capital, astfel incat costul procurării resurselor necesare realizării unei anumite cantităţi de producţie să rămană constant.
Generalizand, procurarea unei unităţi suplimentare de muncă presupune renunţarea la s/a unităţi de capital. In figura 5.4, s/a = 2,5. In faţa raportului trebuie adăugat semnul minus, care semnifică diminuarea cantităţii utilizate dintr-o resursă, atunci cand creşte cantitatea utilizată din cealaltă resursă. –s/a este panta curbei isocost.
Toate cele discutate in acest subcapitol pot fi sintetizate astfel:
La preţuri fixe a şi s ale capitalului şi respectiv ale muncii, cu o sumă fixă C se va putea procura orice combinaţie de capital şi de muncă dată de ecuaţia din relaţia 5.11. Acestei ecuaţii ii corespunde o curbă isocost.
C/a este cantitatea de capital care poate fi procurată dacă nu se cumpără nici o unitate de muncă, iar s/a este panta negativă a curbei isocost.
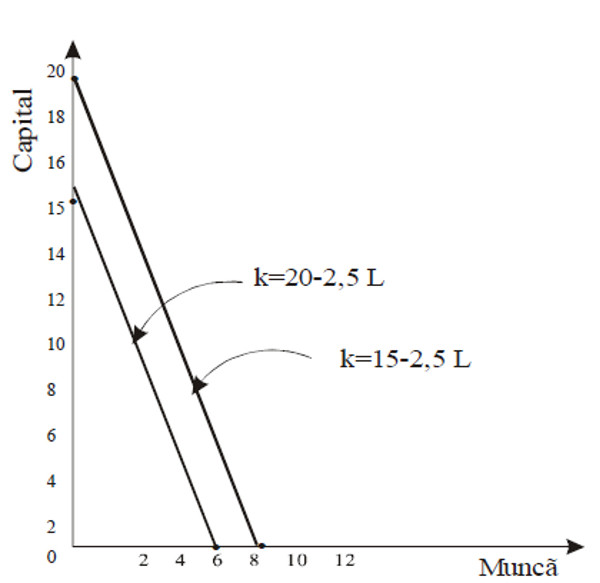
Figura 5.4 Curba isocost atunci cand a = 1.000.000 lei, iar s = 2.500.000 lei.
Producerea cu costuri minime a unei anumite cantităţi de produse
Principiul minimizării costului total necesar producerii unei anumite cantităţi de producţie este ilustrat in figura 5.5. Să presupunem că managementul unei organizaţii doreşte să minimizeze costul total necesar realizării unei producţii de 10000 unităţi. In isocuanta I sunt reprezentate grafic toate combinaţiile de muncă şi de capital cu ajutorul cărora se poate obţine acest nivel de producţie. Preţul muncii „s” este de 40000 lei pe unitate, iar preţul capitalului „a” este de 60000 lei pe unitate. In figura 5.5, sunt prezentate trei dintre nenumăratele curbe isocost care se pot trasa in funcţie de aceste preţuri ale resurselor, ele fiind KM, K'M' şi K"M". Panta tuturor acestor curbe este: s/a = 2/3.
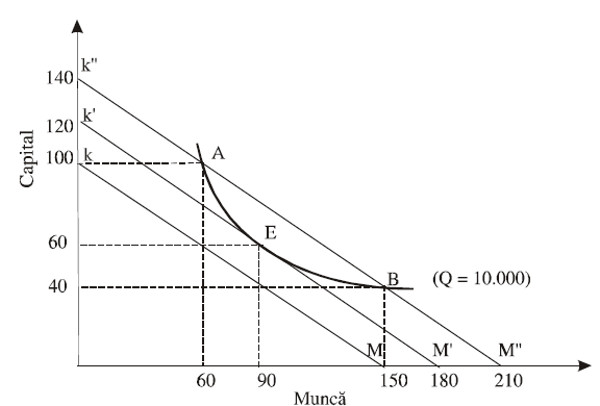
Figura 5.5 Combinaţia optimă de resurse care minimizează costul unei anumite cantităţi de producţie
Curba isocost KM corespunde unui cost de producţie de 6000000 lei. Toate combinaţiile de resurse de pe KM costă 6000000 lei. De exemplu, combinaţia din punctul K la care se utilizează 100 unităţi de capital şi 0 unităţi de muncă costă 6000000 lei (= 60.000 x 100). Similar, se poatecalcula costul asociat curbei K'M' care este de 7200000 lei şi costul asociat curbei K"M" de 8400000 lei.
In vederea realizării cu cost minim a celor 10000 de produse, corespunzătoare isocuantei AB din figura 5.5, managerii vor alege o combinaţie de resurse aflată pe o curbă isocost cat mai apropiată posibil de
origine. Acest obiectiv se atinge atunci cand isocostul este tangent la isocuantă. Din figura 5.5, rezultă că cel mai mic cost cu care se pot realize cele 10000 unităţi corespunde combinaţiei E de resurse de pe curba isocost K'M', şi anume 60 unităţi de capital şi 90 de unităţi de muncă. Costul procurării acestei combinaţii este de 7200000 lei.
sM + aK = 40000 x 90 + 60000 x 60 = 7200000 lei
Nici o altă combinaţie de pe curbele isocost din figură nu poate fi utilizată pentru realizarea celor 10.000 unităţi de producţie. De exemplu, combinaţiile de pe curba isocost KM sunt mai puţin costisitoare decat combinaţia de pe curba isocost K'M'. Dar, după cum se poate observa, cu acestea nu se pot realiza 10.000 unităţi. Pe de altă parte, alte combinaţii cu care se poate realiza producţia de 10.000 unităţi de pe isocuantă, de exemplu A şi B sunt mai scumpe, costand 10.000.000 lei, deci nu corespund cerinţei de minimizare a cheltuielilor.
Prin urmare:
Condiţia de echilibru atunci cand se urmăreşte producerea unei anumite cantităţi, cu costuri minime este:
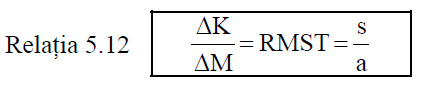
in care:
ΔK = modificarea cantităţii de capital utilizat;
ΔM = modificarea cantităţii de muncă utilizată;
RMST = rata marginală de substituire tehnică;
s = costul unitar al muncii;
a = costul unitar al capitalului.
Avand in vedere că:
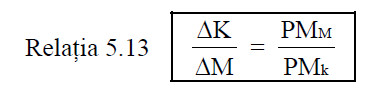
in care:
ΔK = modificarea cantităţii de capital utilizat;
AM = modificarea cantităţii de muncă utilizată;
PMM = produsul marginal al muncii;
PMK = produsul marginal al capitalului.
Combinaţia de resurse este optimă atunci cand:

Această formulă corespunde combinaţiei E. In situaţia combinaţiei A din figura 5.5, panta isocuantei este mai mare decat panta curbei isocost. Avand in vedere că panta isocuantei este PMM/PMK, iar panta isocostului este s/a, in punctul A PMM/PMK > s/a, ceea ce este echivalent cu PMM/s > PMK/a.
De aceea, in punctul A, produsul marginal pe leu cheltuit pentru procurarea ultimei unităţi de muncă este mai mare decat produsul marginal cheltuit pentru procurarea ultimei unităţi de capital.
Pentru ilustrare, să presupunem că in punctul A, PMM este 160, iar PMK este 80. In această situaţie:
PMM/s =160/40 = 4; PMK/a = 80/60 =11,33. Deci, PMM/s > PM/a
Rezultă că, in această situaţie, capitalul trebuie inlocuit cu munca, deoarece aceasta aduce un produs marginal superior pe leu cheltuit. O unitate suplimentară de muncă va contribui la creşterea producţiei cu 160 de unităţi, in condiţiile creşterii costurilor cu 40.000 lei. Pentru a menţine producţia la 10.000 bucăţi, capitalul se va reduce cu 2 unităţi, fapt care va contribui la reducerea costurilor cu 120.000 lei. Prin urmare, efectul agregat al modificării raportului muncă – capital va fi reducerea cu 80.000 lei a costurilor totale.
Acest exemplu demonstrează că pentru a realiza o producţie constantă, atunci cand: PMM/s > PMK/a managerii pot reduce costurile prin creşterea utilizării muncii şi reducerea simultană a utilizării capitalului, conform proporţiei necesare menţinerii constante a producţiei, pană ce se va ajunge la echilibru, deci la egalitatea dintre rapoarte.
In punctul B se inregistrează, aşa cum vom vedea, situaţia inversă. In acest punct, RMST = 40/240 = 1/6, care este mai mic decat s/a = 2/3. In această situaţie PMM = 40, iar PMK = 240. Utilizarea suplimentară a unei unităţi de capital conduce la reducerea muncii cu 6 unităţi in condiţiile menţinerii neschimbate a cantităţii. Costul suplimentar al capitalului va fi 60000 lei, reducerea de cost aferentă muncii este 360000 lei (6 x 60000 lei). Prin urmare, costurile totale se vor reduce cu 300000 lei.
Cele discutate mai sus se pot sintetiza astfel:
Pentru a produce o anumită cantitate de producţie cu costuri minime, prin utilizarea a două resurse (muncă şi capital) al căror preţ se stabileşte pe piaţă, managerul va alege acea combinaţie de resurse pentru care se respectă relaţia:
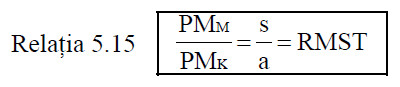
Această condiţie presupune, de asemenea, ca:

In această situaţie de echilibru care conduce la minimizarea costului, isocuanta asociată nivelului dorit al producţiei este tangentă la curba isocost (a cărei pantă este s/a). Condiţia de echilibru presupune, de asemenea, ca produsul marginal pe leu cheltuit pentru procurarea ultimei unităţi să fie acelaşi in cazul ambelor resurse, respectandu-se relaţia 5.16. Dacă PMM/s > PMK/a se va suplimenta consumul de capital pană se atinge echilibrul. Dacă PMM/s < PMK/a se va suplimenta consumul de muncă pană se atinge echilibrul.
Obţinerea unei cantităţi maxime de producţie cu un anumit cost
In majoritatea cazurilor, organizaţiile planifică mai intai ce cantitate de produse vor realiza şi abia după aceea stabilesc combinaţia de resurse prin intermediul căreia pot minimiza costurile. Se poate intalni insă şi situaţia inversă, in care managerii unei organizaţii dispun de o sumă limitată de bani şi işi propun să o utilizeze astfel incat să maximizeze producţia. Acest obiectiv se poate indeplini cu o singură combinaţie de resurse denumită combinaţia optimă de produse, care trebuie determinată. Această situaţie este prezentată in figura 5.6.
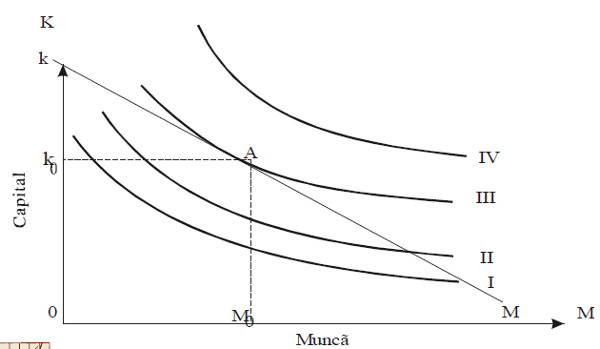
Figura 5.6 Maximizarea producţiei la un nivel dat al costurilor
Linia isocostului KM reprezintă totalitatea combinaţiilor de două resurse care pot fi procurate cu suma de bani de care dispune intreprinderea, in condiţiile date de preţ al resurselor. In figură sunt prezentate patru isocuante. Este evident că la nivelul impus al costului, nivelul producţiei de pe isocuanta IV nu poate fi atins. Nu vor fi alese nici nivelele de producţie de pe isocuantele I şi II, pentru că in condiţiile sumei disponibile se poate aspira la un nivel superior al producţiei. Cel mai inalt nivel al producţiei, posibil de atins in condiţiile restricţiei respective de cost, se poate realize utilizand combinaţia M0 – muncă, K0 – capital. In punctul A, isocuanta III este tangentă cu linia dată a isocostului. In acest punct, pantele celor două curbe trebuie să fie egale. De aceea,
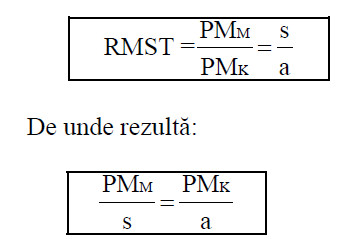
Pentru a vedea de ce, in vederea maximizării producţiei, PMM/s trebuie să fie egal cu PMK/a, să luăm ca exemplu situaţia in care s = 2.000 lei, a = 3.000 lei, PMM = 6 unităţi, PMK = 12 unităţi, caz in care:
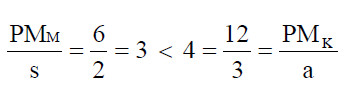
Aceasta inseamnă că ultima unitate de muncă adaugă trei unităţi de producţie pentru fiecare leu cheltuit. Dacă organizaţia doreşte să-şi maximizeze producţia in condiţiile unui anumit cost, trebuie să cheltuiască cu 1.000 lei mai puţin pentru plata muncii, utilizand suma economisită pentru a-şi procura capital suplimentar. In aceste condiţii, se va disponibiliza jumătate de unitate de muncă, iar capitalul utilizat va putea creşte cu 1/3 unităţi. Costul este neschimbat, iar producţia creşte cu o unitate (-6/2 + 12/3). Dacă se continuă reducerea costului cu munca, utilizandu-se economiile pentru a se suplimenta capitalul utilizat, astfel incat costul total să se meanţină constant, produsul marginal al muncii creşte, in timp ce produsul marginal al capitalului scade. De aceea, la un moment dat, inegalitatea se transformă in egalitate.
Cele de mai sus se pot sintetiza astfel:
Combinaţia optimă de resurse, posibil a fi procurată cu o anumită sumă de bani disponibilă, care poate maximiza producţia, este aceea pentru care rata marginală de substituţie tehnică RMST este egală cu raportul dintre preţurile celor două resurse: s/a. Din punct de vedere grafic, această egalitate se poate traduce prin egalitatea dintre pantele isocuantei şi isocostului.
Factori care influenţează combinarea resurselor
Atat in cazul deciziei de producere a unei anumite cantităţi cu costuri minime, cat şi in situaţia cand se urmăreşte obţinerea unei cantităţi maxime de producţie cu un anumit cost, pot interveni modificări in timp, datorită unor factori care influenţează alegerea combinaţiei de resurse utilizate. Principalii factori care influenţează alegerea combinaţiei de resurse cu ajutorul cărora se realizează producţia sunt:
- preţul resurselor
- nivelul tehnologiei.
Modificarea preţului uneia sau a ambelor resurse care contribuie la realizarea producţiei conduce la modificarea echilibrului stabilit anterior. Aşa cum am arătat mai sus, echilibrul se inregistrează atunci cand:
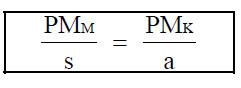
Atunci cand preţul muncii creşte, iar preţul capitalului rămane neschimbat, egalitatea de mai sus se transformă intr-o inegalitate:
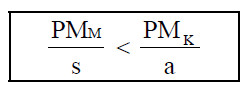
In această situaţie, dacă organizaţia doreşte să producă la acelaşi cost, trebuie să utilizeze mai mult capital şi mai puţină muncă. O decizie similară, dar in sensul creşterii cantităţii de muncă utilizată, trebuie luată atunci cand creşte preţul capitalului.
Modificarea raportului dintre resursele utilizate in producţie, ca urmare a schimbării preţului uneia dintre ele, poartă numele de efect de substituţie.
Alegerea procesului tehnologic precum şi perfecţionarea lui continuă au un rol important in ceea ce priveşte modul cum sunt utilizate resursele.
Procesul tehnologic reprezintă totalitatea operaţiilor care presupun prelucrări mecanice şi chimice, montaj etc. prin intermediul cărora materiile prime, semifabricatele şi materialele sunt transformate in produse finite. Procesul tehnologic prevede materiile prime şi semifabricatele din care se fabrică produsul precum şi calitatea acestora, maşinile şi utilajele folosite in operaţiile de prelucrare şi ansamblul metodelor, procedeelor şi operaţiilor utilizate in vederea obţinerii produsului.
Modificarea tehnologiei presupune o imbunătăţire a nivelului de cunoştinţe cu privire la modul cum trebuie organizaţi factorii de producţie, astfel incat cu oricare dintre combinaţiile de resurse să se producă mai mult decat in trecut. Cand se modifică tehnologia, harta isocuantelor se deplasează spre origine, fiecare combinaţie de resurse putand contribui la producerea unei cantităţi mai mari de produse.
Deci, ca urmare a unei perfecţionări tehnologice, un anumit nivel de producţie se obţine cu o cantitate mai mică de resurse decat in trecut.