Supply Chain Design and Analysis: Models and Methods
- Details
- Category: Supply Chain Management
- Hits: 35,565
For years, researchers and practitioners have primarily investigated the various processes within manufacturing supply chains individually. Recently, however, there has been increasing attention placed on the performance, design, and analysis of the supply chain as a whole.
This attention is largely a result of the rising costs of manufacturing, the shrinking resources of manufacturing bases, shortened product life cycles, the leveling of the playing field within manufacturing, and the globalization of market economies.
The objectives of this paper are to:
- provide a focused review of literature in multi-stage supply chain modeling
- define a research agenda for future research in this area.
A supply chain may be defined as an integrated process wherein a number of various business entities (i.e., suppliers, manufacturers, distributors, and retailers) work together in an effort to:
- acquire raw materials,
- convert these raw materials into specified final products,
- deliver these final products to retailers
This chain is traditionally characterized by a forward flow of materials and a backward flow of information. For years, researchers and practitioners have primarily investigated the various processes of the supply chain individually. Recently, however, there has been increasing attention placed on the performance, design, and analysis of the supply chain as a whole.
From a practical standpoint, the supply chain concept arose from a number of changes in the manufacturing environment, including the rising costs of manufacturing, the shrinking resources of manufacturing bases, shortened product life cycles, the leveling of the playing field within manufacturing, and the globalization of market economies.
The current interest has sought to extend the traditional supply chain to include “reverse logistics”, to include product recovery for the purposes of recycling, re-manufacturing, and re-use. Within manufacturing research, the supply chain concept grew largely out of two-stage multi-echelon inventory models, and it is important to note that considerable progress has been made in the design and analysis of two-echelon systems.
Most of the research in this area is based on the classic work of Clark and Scarf (1960) and Clark and Scarf (1962). The interested reader is referred to Federgruen (1993) and Bhatnagar, et. al. (1993) for comprehensive reviews of models of this type. More recent discussions of two-echelon models may be found in Diks, et. al. (1996) and van Houtum, et. al. (1996). The objectives of this paper are to:
- provide a focused review of literature in the area of multi-stage supply chain design and analysis
- develop a research agenda that may serve as a basis for future supply chain research.
The Supply Chain Defined
As mentioned above, a supply chain is an integrated manufacturing process wherein raw materials are converted into final products, then delivered to customers. At its highest level, a supply chain is comprised of two basic, integrated processes:
- the Production Planning and Inventory Control Process,
- the Distribution and Logistics Process.
These Processes illustrated below in Figure 1, provide the basic framework for the conversion and movement of raw materials into final products.
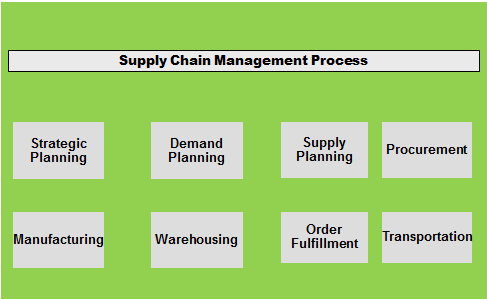
Figure 1. The Supply Chain Process
The Production Planning and Inventory Control Process encompass the manufacturing and storage sub-processes, and their interface(s). More specifically, production planning describes the design and management of the entire manufacturing process (including raw material scheduling and acquisition, manufacturing process design and scheduling, and material handling design and control). Inventory control describes the design and management of the storage policies and procedures for raw materials, work-in-process inventories, and usually, final products.
The Distribution and Logistics Process determines how products are retrieved and transported from the warehouse to retailers. These products may be transported to retailers directly, or may first be moved to distribution facilities, which, in turn, transport products to retailers. This process includes the management of inventory retrieval, transportation, and final product delivery.
These processes interact with one another to produce an integrated supply chain. The design and management of these processes determine the extent to which the supply chain works as a unit to meet required performance objectives.
Literature Review
The supply chain in Figure 1 consists of five stages. Generally, multi-stage models for supply chain design and analysis can be divided into four categories, by modeling approach. In the cases included here, the modeling approach is driven by the nature of the inputs and the objective of the study.
The four categories are:
- deterministic analytical models, in which the variables are known and specified
- stochastic analytical models, where at least one of the variables is unknown and is assumed to follow a particular probability distribution
- economic models
- simulation models
Deterministic Analytical Models
Williams (1981) presents seven heuristic algorithms for scheduling production and distribution operations in an assembly supply chain network (i.e., each station has at most one immediate successor, but any number of immediate predecessors). The objective of each heuristic is to determine a minimum-cost production and/or product distribution schedule that satisfies final product demand.
The total cost is a sum of average inventory holding and fixed (ordering, delivery, or set-up) costs. Finally, the performance of each heuristic is compared using a wide range of empirical experiments, and recommendations are made on the bases of solution quality and network structure.
Williams (1983) develops a dynamic programming algorithm for simultaneously determining the production and distribution batch sizes at each node within a supply chain network. As in Williams (1981), it is assumed that the production process is an assembly process. The objective of the heuristic is to minimize the average cost per period over an infinite horizon, where the average cost is a function of processing costs and inventory holding costs for each node in the network.
Ishii, et. al (1988) develop a deterministic model for determining the base stock levels and lead times associated with the lowest cost solution for an integrated supply chain on a finite horizon. The stock levels and lead times are determined in such a way as to prevent stockout, and to minimize the amount of obsolete (“dead”) inventory at each stock point. Their model utilizes a pull-type ordering system which is driven by, in this case, linear (and known) demand processes.
Cohen and Lee (1989) present a deterministic, mixed-integer, non-linear mathematical programming model, based on economic order quantity (EOQ) techniques, to develop what the authors refer to as a “global resource deployment” policy. More specifically, the objective function used in their model maximizes the total after-tax profit for the manufacturing facilities and distribution centers (total revenue less total before-tax costs less taxes due). This objective function is subject to a number of constraints, including “managerial constraints” (resource and production constraints) and “logical consistency constraints” (feasibility, availability, demand limits, and variable non-negativity).
The outputs resulting from their model include:
- Assignments for finished products and subassemblies to manufacturing plants, vendors to distribution centers, distribution centers to market regions.
- Amounts of components, subassemblies, and final products to be shipped among the vendors, manufacturing facilities, and distribution centers.
- Amounts of components, subassemblies, and final products to be manufactured at the manufacturing facilities.
Moreover, this model develops material requirements and assignments for all products, while maximizing after-tax profits.
Cohen and Moon (1990) extend Cohen and Lee (1989) by developing a constrained optimization model, called PILOT, to investigate the effects of various parameters on supply chain cost, and consider the additional problem of determining which manufacturing facilities and distribution centers should be open. More specifically, the authors consider a supply chain consisting of raw material suppliers, manufacturing facilities, distribution centers, and retailers. This system produces final products and intermediate products, using various types of raw materials.
Using this particular system, the PILOT model accepts as input various production and transportation costs, and consequently outputs:
- Which of the available manufacturing facilities and distribution centers should be open.
- Raw material and intermediate order quantities for vendors and manufacturing facilities.
- Production quantities by-product by the manufacturing facility.
- Product-specific shipping quantities from manufacturing facility to distribution center to the customer.
The objective function of the PILOT model is a cost function, consisting of fixed and variable production and transportation costs, subject to supply, capacity, assignment, demand, and raw material requirement constraints. Based on the results of their example supply chain system, the authors conclude that there are a number of factors that may dominate supply chain costs under a variety of situations and that transportation costs play a significant role in the overall costs of supply chain operations.
Newhart, et. al. (1993) design an optimal supply chain using a two-phase approach. The first phase is a combination of a mathematical program and heuristic model, with the objective of minimizing the number of distinct product types held in inventory throughout the supply chain. This is accomplished by consolidating substitutable product types into single SKUs.
The second phase is a spreadsheet-based inventory model, which determines the minimum amount of safety stock required to absorb demand and lead time fluctuations. The authors considered four facility location alternatives for the placement of the various facilities within the supply chain. The next step is to calculate the amount of inventory investment under each alternative, given a set of demand requirements, and then select the minimum cost alternative.
Arntzen, et. al. (1995) develop a mixed integer programming model, called Global Supply Chain Model (GSCM), that can accommodate multiple products, facilities, stages (echelons), time periods, and transportation modes. More specifically, the Global Supply Chain Model (GSCM) minimizes a composite function of:
- activity days
- total (fixed and variable)cost of production, inventory, material handling, overhead, and transportation costs.
The model requires, as input, bills of materials, demand volumes, costs and taxes, and activity day requirements and provides, as output:
- the number and location of distribution centers
- the customer-distribution center assignment
- the number of echelons (amount of vertical integration)
- the product-plant assignment.
Voudouris (1996) develops a mathematical model designed to improve efficiency and responsiveness in a supply chain. The model maximizes system flexibility, as measured by the time-based sum of instantaneous differences between the capacities and utilization of two types of resources: inventory resources and activity resources. Inventory resources are resources directly associated with the amount of inventory held; activity resources, then, are resources that are required to maintain material flow.
The model requires, as input, product-based resource consumption data and bill-of-material information, and generates, as output:
- a production, shipping, and delivery schedule for each product
- target inventory levels for each product.
Camm, et. al. (1997) develop an integer programming model, based on an uncapacitated facility location formulation, for Procter and Gamble Company. The purpose of the model is to: (1) determine the location of distribution centers (DCs) and (2) assign those selected DCs to customer zones. The objective function of the model minimizes the total cost of the DC location selection and the DC-customer assignment, subject to constraints governing DC-customer assignments and the maximum number of DCs allowed.
Stochastic Analytical Models
Cohen and Lee (1988) develop a model for establishing a material requirements policy for all materials for every stage in the supply chain production system. In this work, the authors use four different cost-based sub-models (there is one stochastic sub-model for each production stage considered).
Each of these sub-models is listed and described below :
- Material Control: Establishes material ordering quantities, reorder intervals, and estimated response times for all supply chain facilities, given lead times, fill rates, bills of material, cost data, and production requirements.
- Production Control: Determines production lot sizes and lead times for each product, given material response times.
- Finished Goods Stockpile (Warehouse): Determines the economic order size and quantity for each product, using cost data, fill rate objectives, production lead times, and demand data.
- Distribution: Establishes inventory ordering policies for each distribution facility, based on transportation time requirements, demand data, cost data, network data, and fill rate objectives.
Each of these sub-models is based on a minimum-cost objective. In the final computational step, the authors determine approximate optimal ordering policies using a mathematical program, which minimizes the total sum of the costs for each of the four sub-models.
Svoronos and Zipkin (1991) consider multi-echelon, distribution-type supply chain systems (i.e., each facility has at most one direct predecessor, but any number of direct successors). In this research, the authors assume a base stock, one-for-one (S-1, S) replenishment policy for each facility, and that demands for each facility follow an independent Poisson process.
The authors obtain steady-state approximations for the average inventory level and the average number of outstanding backorders at each location for any choice of base stock level. Finally, using these approximations, the authors propose the construction of an optimization model that determines the minimum-cost base stock level.
Lee and Billington (1993) develop a heuristic stochastic model for managing material flows on a site-by-site basis. Specifically, the authors model a pull-type, periodic, order- up-to inventory system, and determine the review period (by product type) and the order- up-to quantity (by product type) as model outputs.
The authors develop a model which will either:
- determine the material ordering policy by calculating the required stock levels to achieve a given target service level for each product at each facility
- determine the service level for each product at each facility, given a material ordering policy.
Lee, et. al. (1993), develop a stochastic, periodic-review, order-up-to inventory model to develop a procedure for process localization in the supply chain. That is, the authors propose an approach to operational and delivery processes that consider differences in target market structures (e.g., differences in language, environment, or governments).
Thus, the objective of this research is to design the product and production processes that are suitable for different market segments that result in the lowest cost and highest customer service levels overall.
Pyke and Cohen (1993) develop a mathematical programming model for an integrated supply chain, using stochastic sub-models to calculate the values of the included random variables included in the mathematical program. The authors consider a three-level supply chain, consisting of one product, one manufacturing facility, one warehousing facility, and one retailer. The model minimizes total cost, subject to a service level constraint, and holds the set-up times, processing times, and replenishment lead times constant. The model yields the approximate economic (minimum cost) reorder interval, replenishment batch sizes, and the order-up-to product levels (for the retailer) for a particular production network.
Pyke and Cohen (1994) follow Pyke and Cohen (1993) research by including a more complicated production network. In Pyke and Cohen (1994), the authors again consider an integrated supply chain with one manufacturing facility, one warehouse, and one retailer, but now consider multiple product types. The new model yields similar outputs; however, it determines the key decision variables for each product type. More specifically, this model yields the approximate economic (minimum cost) reorder interval (for each product type), replenishment batch sizes (for each product type), and the order- up-to product levels (for the retailer, for each product type) for a particular supply chain network.
Tzafestas and Kapsiotis (1994) utilize a deterministic mathematical programming approach to optimize a supply chain, then use simulation techniques to analyze a numerical example of their optimization model.
In this work, the authors perform the optimization under three different scenarios :
- Manufacturing Facility Optimization: Under this scenario, the objective is to minimize the total cost incurred by the manufacturing facility only; the costs experienced by other facilities are ignored.
- Global Supply Chain Optimization: This scenario assumes a cooperative relationship among all stages of the supply chain, and therefore minimizes the total operational costs of the chain as a whole.
- Decentralized Optimization: This scenario optimizes each of the supply chain components individually, and thus minimizes the cost experienced by each level.
The authors observe that for their chosen example, the differences in total costs among the three scenarios are very close.
Towill and Del Vecchio (1994) consider the application of filter theory and simulation to the study of supply chains. In their research, the authors compare the filter characteristics of supply chains to analyze various supply chain responses to randomness in the demand pattern. These responses are then compared using simulation, in order to specify the minimum safety stock requirements that achieve a particular desired service level.
Lee and Feitzinger (1995) develop an analytical model to analyze product configuration for postponement (i.e., determining the optimal production step for product differentiation), assuming stochastic product demands. The authors assume a manufacturing process with I production steps that may be performed at a factory or at one of the M distribution centers (DCs).
The problem is to determine a step P such that steps 1 through P will be performed at the factory and steps (P+1) to I will be performed at the DCs. The authors solve this problem by calculating an expected cost for the various product configurations, as a sum of inventory, freight, customs, setup, and processing costs. The optimal value of P is the one that minimizes the sum of these costs.
Altiok and Ranjan (1995) consider a generalized production/inventory system with: M
(M > 1) stages (j = 1,...M), one type of final product, random processing times (FIFO, for all stages) and set-up times, and intermediate buffers. The system experiences demand for finished products according to a compound Poisson process, and the inventory levels for inventories (intermediate buffers and finished goods) are controlled according to a continuous review (R,r) inventory policy, and backorders are allowed.
The authors develop an iterative procedure wherein each of the two-node sub-systems is analyzed individually; the procedure terminates once the estimate average throughput for each sub-system is all approximately equal. Once the termination condition is met, the procedure allows for the calculation of approximate values for the two performance measures:
- the inventory levels in each buffer j,
- the backorder probability.
The authors conclude that their approximation is acceptable as long as the P(backorder) does not exceed 0.30, in which cases the system is failing to effectively accommodate demand volumes.
Finally, Lee, et. al. (1997) develop stochastic mathematical models describing “The Bullwhip Effect”, which is defined as the phenomenon in which the variance of buyer demand becomes increasingly amplified and distorted at each echelon upwards throughout the supply chain. That is, the actual variance and magnitude of the orders at each echelon is increasingly higher than the variance and magnitude of the sales, and that this phenomenon propagates upstream within the chain. In this research, the authors develop stochastic analytical models describing the four causes of the bullwhip effect (demand signal processing, rationing game, order batching, and price variations), and show how these causes contribute to the effect.
Economic Models
Christy and Grout (1994) develop an economic, game-theoretic framework for modeling the buyer-supplier relationship in a supply chain. The basis of this work is a 2 x 2 supply chain “relationship matrix”, which may be used to identify conditions under which each type of relationship is desired. These conditions range from high to low process specificity, and from high to low product specificity.
Thus, the relative risks assumed by the buyer and the supplier are captured within the matrix. For example, if the process specificity is low, then the buyer assumes the risk; if the product specificity is low, then the supplier assumes the risk. For each of the four quadrants (and therefore, each of the four risk categories), the authors go on to assign appropriate techniques for modeling the buyer-supplier relationship. For the two-echelon case, the interested reader is referred to Cachon and Zipkin (1997).
Simulation Models
Towill (1991) and Towill, et. al. (1992) use simulation techniques to evaluate the effects of various supply chain strategies on demand amplification. The strategies investigated are as follows :
- Eliminating the distribution echelon of the supply chain, by including the distribution function in the manufacturing echelon.
- Integrating the flow of information throughout the chain.
- Implementing a Just-In-Time (JIT) inventory policy to reduce time delays.
- Improving the movement of intermediate products and materials by modifying the order quantity procedures.
- Modifying the parameters of the existing order quantity procedures.
The objective of the simulation model is to determine which strategies are the most effective in smoothing the variations in the demand pattern. The just-in-time strategy (strategy (3) above) and the echelon removal strategy (strategy (1) above) were observed to be the most effective in smoothing demand variations.
Wikner, et. al. (1991) examine five supply chain improvement strategies, then implement these strategies on a three-stage reference supply chain model. The five strategies are :
- Fine-tuning the existing decision rules.
- Reducing time delays at and within each stage of the supply chain.
- Eliminating the distribution stage from the supply chain.
- Improving the decision rules at each stage of the supply chain.
- Integrating the flow of information, and separating demands into “real” orders, which are true market demands, and “cover” orders, which are orders that bolster safety stocks.
Their reference model includes a single factory (with an on-site warehouse), distribution facilities, and retailers. Thus, it is assumed that every facility within the chain houses some inventory. The implementation of each of the five different strategies is carried out using simulation, the results of which are then used to determine the effects of the various strategies on minimizing demand fluctuations. The authors conclude that the most effective improvement strategy is strategy (5), improving the flow of information at all levels throughout the chain, and separating orders.
Supply Chain Performance Measures
An important component in supply chain design and analysis is the establishment of appropriate performance measures. A performance measure, or a set of performance measures, is used to determine the efficiency and/or effectiveness of an existing system, or to compare competing alternative systems. Performance measures are also used to design proposed systems, by determining the values of the decision variables that yield the most desirable level(s) of performance. Available literature identifies a number of performance measures as important in the evaluation of supply chain effectiveness and efficiency. These measures, described in this Section, may be categorized as either qualitative or quantitative.
Qualitative Performance Measures
Qualitative performance measures are those measures for which there is no single direct numerical measurement, although some aspects of them may be quantified. These objectives have been identified as important, but are not used in the models reviewed here:
Customer Satisfaction: The degree to which customers are satisfied with the product and/or service received, and may apply to internal customers or external customers. Customer satisfaction is comprised of three elements :
- Pre-Transaction Satisfaction: satisfaction associated with service elements occurring prior to product purchase.
- Transaction Satisfaction: satisfaction associated with service elements directly involved in the physical distribution of products.
- Post-Transaction Satisfaction: satisfaction associated with support provided for products while in use.
Flexibility: The degree to which the supply chain can respond to random fluctuations in the demand pattern.
Information and Material Flow Integration: The extent to which all functions within the supply chain communicate information and transport materials.
Effective Risk Management: All of the relationships within the supply chain contain inherent risk. Effective risk management describes the degree to which the effects of these risks is minimized.
Supplier Performance: With what consistency suppliers deliver raw materials to production facilities on time and in good condition.
Quantitative Performance Measures
Quantitative performance measures are those measures that may be directly described numerically. Quantitative supply chain performance measures may be categorized by:
- objectives that are based directly on cost or profit
- objectives that are based on some measure of customer responsiveness.
Measures Based on Cost
- Cost Minimization: The most widely used objective. Cost is typically minimized for an entire supply chain (total cost), or is minimized for particular business units or stages.
- Sales Maximization: Maximize the amount of sales dollars or units sold.
- Profit Maximization : Maximize revenues less costs.
- Inventory Investment Minimization: Minimize the amount of inventory costs (including product costs and holding costs)
- Return on Investment Maximization: Maximize the ratio of net profit to capital that was employed to produce that profit.
Measures Based on Customer Responsiveness
- Fill Rate Maximization: Maximize the fraction of customer orders filled on time.
- Product Lateness Minimization: Minimize the amount of time between the promised product delivery date and the actual product delivery date.
- Customer Response Time Minimization: Minimize the amount of time required from the time an order is placed until the time the order is received by the customer. Usually refers to external customers only.
- Lead Time Minimization: Minimize the amount of time required from the time a product has begun its manufacture until the time it is completely processed.
- Function Duplication Minimization: Minimize the number of business functions that are provided by more than one business entity.
Performance Measures Used in Supply Chain Modeling
As mentioned above, an important element in supply chain modeling is the establishment of appropriate performance measures. Each of the models reviewed in Section 3 sought to optimize one or more measures of supply chain performance, given a set of physical or operational system constraints. Table 1 below summarizes the performance measures used in the reviewed research.
| Basis | Performance Measure |
Author(s) |
| Cost | Minimize cost | Camm, et. al. (1997) Lee, et. al. (1997) Lee and Feitzinger (1995) Tzafestas and Kapsiotis (1994) Pyke and Cohen (1994) Pyke and Cohen (1993) Lee, et. al. (1993) Svoronos and Zipkin (1991) Cohen and Moon (1990) Cohen and Lee (1988) Ishii, et. al. (1988) Williams (1983) Williams (1981) |
| Minimize average inventory levels | Altiok and Ranjan (1995) Towill and Del Vecchio (1994) | |
| Maximize profit | Cohen and Lee (1989) | |
| Minimize amount of obsolete inventory | Ishii, et. al. (1988) | |
| Customer Responsiveness | Achieve target service level (fill rate) | Lee and Billington (1993) Lee, et. al. (1993) Towill and Del Vecchio (1994) |
| Minimize stockout probability | Altiok and Ranjan (1995) Ishii, et. al. (1988) | |
| Cost and Customer Responsiveness | Minimize product demand variance or demand amplification | Newhart, et. al (1993) Towill, et. al. (1992) Towill (1991) Wikner, et. al. (1991) |
| Maximize buyer-supplier benefit | Christy and Grout (1994) | |
| Cost and Activity Time | Minimize the number of activity days and total cost | Arntzen, et. al (1995) |
| Flexibility | Maximize available system capacity | Voudouris (1996) |
Table 1. Performance Measures in Supply Chain Modeling
Decision Variables in Supply Chain Modeling
In supply chain modeling, the performance measures (such as those described in Section 4) are expressed as functions of one or more decision variables. These decision variables are then chosen in such a way as to optimize one or more performance measures.
The decision variables used in the reviewed models are described below.
- Production/Distribution Scheduling: Scheduling the manufacturing and/or distribution.
- Inventory Levels: Determining the amount and location of every raw material, subassembly, and final assembly storage.
- Number of Stages (Echelons): Determining the number of stages (or echelons) that will comprise the supply chain. This involves either increasing or decreasing the chain’s level of vertical integration by combining (or eliminating) stages or separating (or adding) stages, respectively.
- Distribution Center (DC) - Customer Assignment: Determining which DC(s) will serve which customer(s).
- Plant - Product Assignment: Determining which plant(s) will manufacture which product(s).
- Buyer-Supplier Relationships: Determining and developing critical aspects of the buyer-supplier relationship.
- Product Differentiation Step Specification: Determining the step within the process of product manufacturing at which the product should be differentiated (or specialized).
- The number of Product Types Held in Inventory: Determining the number of different product types that will be held in finished goods inventory.
Research Agenda
The models reviewed here, and summarized above in Table 1, utilize a number of the performance measures identified in Sections 4.1 and 4.2. Table 2 summarizes the reviewed research.
For each of the models studied, the table illustrates:
- the type(s) of modeling methodology used
- the performance measure(s) used,
- the decision variable(s) used to optimize the associated performance measure(s).
The approach and scope of existing research in the design and analysis of supply chains illustrate a number of issues that have not yet been addressed in the literature. This section suggests a research agenda for supply chain design and analysis in:
- the evaluation and development of supply chain performance measures,
- the development of models and procedures to relate decision variables to the performance measures,
- consideration of issues affecting supply chain modeling,
- the classification of supply chain systems to allow for the development of rules-of-thumb or general techniques to aid in the design and analysis of manufacturing supply chains.
Supply Chain Performance Measures
Table 1 identifies the performance measures that have been used in the literature. These measures and others may be appropriate for supply chain design and analysis.
Available research has not specifically addressed the adequacy or appropriateness of existing supply chain performance measures.
More specifically, the research questions that may be answered are:
-
Are the existing performance measures appropriate for supply chains? It is unlikely that a single performance measure will be adequate for an entire supply chain (the interested reader is referred to Beamon (1996) for an evaluation of supply chain performance measures). It is more likely that a system or function of performance measures will be necessary for the accurate and inclusive measurement of supply chain systems.
-
What are the appropriate performance measures for supply chains? That is, what types of performance measures or performance measurement systems are appropriate for supply chain performance analysis, and why?
Supply Chain Optimization
An important component in supply chain design is determining how an effective supply chain design is achieved, given a performance measure, or a set of performance measures. Research in supply chain modeling has only scratched the surface of how supply chain strategies (or decision variables) may affect a given performance measure, or a set of performance measures. Lee and Whang (1993) and Chen (1997) are examples of such research.
Lee and Whang (1993) develop a performance measurement system that attempts to match the performance metric of individual supply chain managers with those of the entire supply chain, in an attempt to minimize the total loss associated with conflicting goals. Similarly, Chen (1997) also investigates the relationship between individual supply chain managers and the supply chain as a whole, but does so on the basis of inventory costs. In this work, Chen (1997) seeks to develop optimal inventory decision rules for managers (who have only local information) that result in the minimum long-run average holding and backorder costs for the entire system.
Table 2 indicates that the majority of the models use the inventory level as a decision variable and cost as a performance measure. However, as also indicated in Table 2, there are a number of other decision variables (and perhaps others that have not yet been studied) that may be appropriately linked to a system of performance measures comprised of measures listed in Table 2 and perhaps others that have not yet been studied. Thus, research is needed that associates appropriate performance measurement systems to critical supply chain decision variables.
Supply Chain Modeling Issues
In supply chain modeling, there are a number of issues that are receiving increasing attention, as evidenced by their prevalent consideration in the work reviewed here.
These issues are:
- product postponement,
- global versus single-nation supply chain modeling
- demand distortion and variance amplification.
Product Postponement
Product postponement is the practice of delaying one or more operations to a later point in the supply chain, thus delaying the point of product differentiation. There are numerous potential benefits to be realized from postponement, one of the most compelling of which is the reduction in the value and amount of held inventory, resulting in lower holding costs.
There are two primary considerations in developing a postponement strategy for a particular end-item:
- determining how many steps to postpone
- determining which steps to postpone.
Current research addressing postponement strategy includes Lee and Feitzinger (1995) and Johnson and Davis (1995).
Global vs. Single-Nation Supply Chain Modeling
Global Supply Chains (GSC) are supply chains that operate (i.e., contain facilities) in multiple nations. When modeling GSCs, there are additional considerations affecting SC performance that are not present in supply chains operating in a single nation. Export regulations, duty rates, and exchange rates are a few of the additional necessary considerations when modeling GSCs. Kouvelis and Gutierrez (1997), Arntzen, et. al. (1995) and Cohen and Lee (1989) address modeling issues associated with GSCs.
Demand Distortion and Variance Amplification
Demand distortion is the phenomenon in which “orders to the supplier have a larger variance than sales to the buyer” and variance amplification occurs when the distortion of the demand “propagates upstream in the amplified form”. These phenomena (also known collectively as the “bullwhip effect” or “whiplash effect”) are common in supply chain systems and were observed as early as Forrester (1961). The consequences of the bullwhip effect on the supply chain may be severe, the most serious of which is excess inventory costs.
As a result, a number of strategies have been developed to counteract the effects of demand distortion and variance amplification. A detailed discussion of the issues and strategies associated with the bullwhip effect may be found in Lee, et. al. (1997), Towill (1996), Newhart, et. al. (1993), Towill, et. al. (1992), Towill (1991), Wikner, et. al. (1991), and Houlihan (1987).
Supply Chain Classification
Supply chain systems are inherently complex. Thus, the models and methods used to accurately study these systems are, expectedly, also complex. However, if supply chain systems could be classified on the bases of specific characteristics, such as uncertainty or volume of demand, number of echelons, or number of items produced, there may be rule-of-thumb techniques that suggest operational characteristics that may achieve a certain objective (or set of objectives). Thus, research that develops a meaningful classification scheme for supply chain systems that leads to rules-of-thumb associations between decision variables and performance objectives is needed.
Summary
A supply chain is defined as a set of relationships among suppliers, manufacturers, distributors, and retailers that facilitates the transformation of raw materials into final products. Although the supply chain is comprised of a number of business components, the chain itself is viewed as a single entity. Traditionally, practitioners and researchers have limited their analyses and scope to individual stages within the larger chain, but have recently identified a need for a more integrated approach to manufacturing system design. Consequently, the supply chain framework has emerged as an important component of this new, integrated approach.
The objective of this paper was twofold:
- to provide a focused review of literature in supply chain modeling
- to identify a research agenda for future research in this area.
More specifically, this paper reviewed the available supply chain models and methods and identified topics for future research consideration that will facilitate the advancement of knowledge and practice in the area of supply chain design and analysis. Based on the existing body of research in supply chain modeling, suggestions were made for future research in the following four areas:
- evaluation and development of supply chain performance measures,
- development of models and procedures to relate decision variables to the performance measures,
- consideration of issues affecting supply chain modeling,
- classification of supply chain systems to allow for the development of rules-of-thumb or general techniques to aid in the design and analysis of manufacturing supply chains.