The Unfinished Research Agenda

There are a number of important questions about business cycles which remain to be answered conclusively. They include the following:

• Are there long cycles coexisting with the business cycle? If there are, then the practice of treating business cycles as ‘growth cycles’ (i.e. fluctuations around a linear or log linear growth trend) will be misleading. This practice is also dubious if the trend itself is stochastic or nonlinear, as noted in section The Long Swing Hypothesis and the Growth Trend .

• Is the cycle endogenously or exogenously generated or, alternatively, what are the relative roles of the economic propagation mechanism and exogenous and internal shocks in cycle generation?
• Have major structural, institutional or policy changes, or shocks, made it necessary to analyse business cycles pertaining to different historical periods separately?
• Is the business cycle real or monetary in origin, or is it caused by a complex interplay of real and monetary factors?
• Is the cycle the result of the process of capitalist development?
• What role has the growth of the government sector, which may be seen as a natural result of capitalist development, played in attenuating, and perhaps even generating, post-war cycles?
• Are there key nonlinearities in the economic system or can linear propagation models be employed for cycle analysis?

The major conclusions of the 1967 conference, reviewed in section: Has the Business Cycle Changed Since 1945? , were that post-war cycles had become ‘growth cycles’ and were different in nature from pre-war cycles. It was also accepted that as a result of alternation between inflation and unemployment policies, in response to political considerations, governments had aggravated cycles but that stabilisation policy was feasible and may have been responsible for the change in the nature of the cycle in the post-war period.

The conference papers reported in Hickman (ed.) (1972) aimed to test the cyclical properties of quarterly models of the US economy. There was some testing of whether cycles were endogenous or exogenous, but it was of limited scope since all the competing hypotheses were really based on the Frisch I or the Slutsky hypothesis.

There was no systematic testing of endogenous cycle theories. The only business cycle theory incorporated in the essentially Keynesian models reflected multiplier-accelerator interaction and inventory considerations and, therefore, concentrated on the goods market. Despite the presence of nonlinear parameter restrictions, there were no major functional (type II) nonlinearities or ‘billiard table’ (type I) nonlinearities1 in the models.

The systematic econometric testing of cycle theories envisaged by Tinbergen (1942) and Koopmans (1947) was not evident in the papers in Hickman (ed.) (1972). No attempt was made to incorporate alternative cycle hypotheses into the models and test their validity. Tinbergen (1942, p. 129) believed that the ultimate scope of econometric testing of cycle theories:

would be that we could state for any theory: (1) whether or not it is in accordance with the facts; and (2) if it were true, to what extent it explains the course of events. The decision that a theory is true can only be taken on economic arguments, but provided that the statistician has not found it to be contrary to the facts. That decision once taken, the statistician may again take over the job and tell (c.f. point (2) above) to what extent it influences the course of events.

Given the nascent state of the art of econometrics, Tinbergen was unable to achieve his ideal. With the larger amount of data available, the higher technical ability of the profession, the much improved computer capabilities and the larger number of competing hypotheses, the time has now come to attempt what Tinbergen suggested. The approach advocated by Tinbergen (1951) was to set up cycle-generating models for each sector of the economy and to link them in an overall model. It would then be possible to see if the sectoral models were in accordance with the facts and measure the contribution to cyclical variation of each sector.

The Hickman (ed.) (1972) conference papers were lacking in this respect because the models were taken as adequate and concentration was trained on the required external influences to generate cycles that mimicked those observed. Random shocks did not do the job in most cases but autoregressive (AR) shocks did.

This set a dangerous precedent because it looked to exogenous cycle generation without adequate testing of endogenous cycle theories. Further, AR shocks are difficult to interpret without a coherent theory of shock generation, which was not presented. Despite the fact that the AR shocks might represent mis-specification errors, the approach, if followed to its conclusion, would lead us to search for the shock generation process that provided the best simulations, taking the propagation model as correct.

The analysis would be purely statistical and would not advance our understanding of the economy. In the absence of good a priori reasons to expect AR shocks, it is likely that the AR shocks are the result of misspecification and indicate the need to improve model specification and our understanding of the economy. The other question touched upon at the conference was that of the role of exogenous variables in cycle generation.

The 1970 conference, reviewed in section: Has the Business Cycle Changed Since 1945? , confirmed that business cycles were not obsolete but had changed to ‘growth cycles’ in the postwar period. Methods of measuring growth cycles were proposed and the forecasting and simulation results were consistent with the findings of Bronfenbrenner (ed.) (1969) and Hickman (ed.) (1972) and were derived in a similar manner to those reported in Hickman. There was no evidence of systematic testing of cycle theories.

If the need to incorporate AR shocks to simulate realistic cycles is interpreted as symptomatic of a misspecification of the lag structure, then one of two routes can be followed to improve the lag specification: further theoretical analysis; or use of data-based techniques. The latter approach was foreseen by Griliches (1967), who noted that such an approach would ask an awful lot of the data. Further, Boch, Yancey and Judge (1973a, b) warn against the biases resulting from repeated testing from the same data base. Nevertheless, this is essentially the approach taken by users of VAR models in the 1980s.

The 1984 conference, reviewed in section Has the Business Cycle Changed Since 1945? , tried to identify the causes of the post-war changes in the US business cycle. Attempts were made to identify the major sources and the nature of shocks and to gauge the impact of institutional, structural and policy changes.

Particular attention was paid to the impacts of the growth in the proportion of government expenditure in GNP, automatic stabilisers and discretionary demand management policy. Generally, it updated information on the themes that occupied the 1967 and 1970 conferences while drawing attention to the importance of supply side shocks since the early 1970s. The Frisch-Slutsky view of a cycle driven by shocks remained unchallenged, and the abandonment of essentially linear large scale econometric models in favour of linear VAR models was illustrated by the fact that the results in only one paper were derived from a large scale econometric model.

The role of nonlinearity has largely been ignored because the size of the large quarterly econometric models of the 1970s encouraged the minimisation of problems arising from nonlinearity. The subsequently popular VAR models in turn assume linearity in order to make use of linear time series techniques. Nonlinear techniques have, however, advanced and the problem of nonlinear estimation is no longer so forbidding.

Blatt (1978) expresses concern about the econometric procedures that have been used to test the cycle specification of econometric models. He notes that because the models tested2 are essentially linear in variables, the type of deterministic solution is severely restricted and if any cycles are produced at all, they are likely to be damped or explosive. In the linear deterministic case the third possibility is that a conservative oscillation will result, but this becomes explosive when shocks are introduced.

Blatt (1986) notes that the range of possibilities is greater for nonlinear models and argues that nonlinearities are strongly indicated by the finding of asymmetry between expansion and contraction phases of the cycle,1 which cannot be explained by stable models that are linear in deviations from trend regardless of the size or the autocorrelation properties of the shocks to the model.

Blatt (1978) argues that following past econometric testing, it has been accepted that the economy is stable and the cycle must be generated by exogenous processes. There are a number of possibilities. Oscillations could be forced. Damped cycles could be produced by the propagation model and kept alive by random shocks. Finally there could be monotonic damped adjustment which converts shocks into a recurrent, but not precisely periodic, oscillation. He believes that such a view has conditioned the methods of testing and he shows some errors that can result.

Blatt (1978) considers a Hicks-type (Hicks 1950) nonlinear deterministic model with type I nonlinearities, in the form of ceilings and floors. A best fit for a linearised version of the model is derived using standard econometric techniques. Simulation experiments with the estimated model reveal it to be stable and yet the data used to estimate the linearised model was generated by the nonlinear model with assumed parameter values imposed to ensure that it generated an exact periodic cycle.

Further, the nonlinear model was shown to be highly unstable. Thus Blatt started with a completely deterministic model which is highly unstable and fitted a stable linear model, in which the economy is driven through the cycle by random shocks. Blatt (1978, pp.298-9) identifies the basic source of the result as the substitution of a linear for a nonlinear equation and argues that:

. . mathematically any linear (or nearly linear) model is fundamentally different from essentially nonlinear models. Introduce as many endogenous or exogenous variables as you wish; introduce as complicated a lag structure as can be imagined it makes no difference. If the structural equations are linear (or nearly so), then results similar to the ones of our calculation must emerge.

Thus existing tests, in disallowing nonlinearities, are failing to consider a large and growing number of cycle hypotheses, and linear econometric techniques applied to linear formulations in a nonlinear world are likely to arrive at incorrect conclusions. Nonlinear specifications should be allowed to compete on an equal basis in the testing of business cycle theories.

Verdoorn and Post (1964) provide one of the few tests of nonlinear cycle theory. Concentrating on labour as the limiting factor, they test for the existence and effects of a ceiling in the Dutch economy. They note that introducing a ceiling implies the introduction of curvilinearity into what may otherwise be a linear model, because a ceiling usually foreshadows its existence before output has reached its maximum.

A continuous curvilinear relationship is, therefore, postulated and a double log transformation is selected from three alternatives considered. With the nonlinearity included, their model displays damped oscillations in expenditure variables. Cyclical fluctuations are more pronounced for value variables and prices, for which the dampening of cyclical movements takes longer. The introduction of nonlinearity, therefore, resulted in damped oscillations in the propagation model but not in a self-sustaining limit cycle (see section: Nonlinear Cycle Theory).

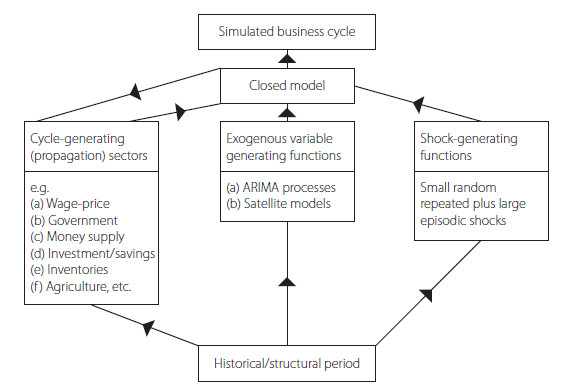
Figure 5.1 An iterative approach to business cycle modeling

The broad conclusion is that despite the increasing sophistication of the econometric and time series techniques used for analysing economic time series, very few of the cycle hypotheses implicit in the business cycle literature have been formulated and adequately tested. Too many things have been allowed to vary at once or have been precluded from testing by the linearity hypothesis. The linearity assumption may also have clouded the picture by encouraging (log) linear trend fitting and the separation of business cycle and growth analysis.

The previous discussion suggests an approach to modelling which can be outlined as follows. The model of the macroeconomy should be broken down into its main structural sectors, and shock-generating and exogenous variable generating models should be appended. The exogenous variables may themselves be cyclical or subject to shocks and might best be modelled using ARIMA generating processes or satellite models.

The choice of structural sectors would be guided by the block recursive features of the model and particular attention should be paid to the potential cycle-propagating features, indicated by the theoretical business cycle literature, of each sector. As suggested by Tinbergen (1939), the different theories of cycle generation could then be tested using various combinations of alternative specifications of these sectors and evaluating their contributions to the explanation of the variance in the economic time series.

Using such a framework (see Figure 5.1), an attempt could be made to answer some of the questions posed at the beginning of this chapter. Both time series and econometric techniques and approaches would have roles to play, and economic historical analysis would also make a contribution by identifying structurally different periods for analysis.