From standard finance to behavioural finance
- Details
- Category: Finance
- Hits: 14,097
Standard finance stand on the arbitrage principles of Miller & Modigliani, the portfolio principles of Markowitz, the capital asset pricing theory of Sharpe, Lintner & Black, and the option-pricing theory of Black, Scholes & Merton.
These approaches consider markets to be efficient and are highly normative and analytical.
Modern financial economic theory is based on the assumption that the representative market actor in the economy is rational in two ways: the market actor makes decisions according to the axiom of expected utility theory and makes unbiased forecasts about the future. According to the expected utility theory, a person is risk-averse and the utility function of a person is concave, i.e. the marginal utility of wealth decreases.
Assets prices are set by rational investors and, consequently, rationality based market equilibrium is achieved. In this equilibrium, securities are priced according to the efficient market hypothesis. This hypothesis will be presented in section 2.2 but first, we will look briefly at the economic decision-making process for the viewpoint of the individual human.
Individual economic decision-making
In traditional economics, the decision-maker is typically rational and self-interested. This is the Homo economicus view of man’s behavior in which a man acts to obtain the highest possible well-being for himself given available information about opportunities and other constraints on his ability to achieve his predetermined goals (Persky, 1995). According to conventional economics, emotions and other extraneous factors do not influence people when it comes to making economic choices.
Homo economicus is seen as “rational”2 in the sense that well-being, as defined by the personal utility function, is optimized given perceived opportunities. That is, the individual seeks to attain very specific and predetermined goals to the greatest extent with the least possible cost.
In most cases, however, this assumption doesn’t reflect how people behave in the real world. The fact is people frequently behave irrationally. Consider how many people purchase lottery tickets in the hope of hitting the big jackpot.
From a purely logical standpoint, it does not make sense to buy a lottery ticket when the odds of winning are overwhelming against the ticket holder (roughly 1 in 146 million, or 0.0000006849%, for the famous Powerball jackpot). Despite this, millions of people spend countless Euros on this activity. These anomalies prompted academics to look to cognitive psychology to account for the irrational and illogical behaviors that modern economics had failed to explain.
The Decision-Making Process – Choice under Uncertainty
When referring to single-decision problems, it has become a practice in normative theoretical models to divide the decision-making process into four steps. Although these steps may not always be followed explicitly, the subdivision of the process in decision-making into steps is useful in an analytical sense.
The four steps are:
- First, one recognizes the present situation or state.
- Second, one evaluates action candidates or options in terms of how much reward or punishment each potential choice would bring.
- Third, one acts in reference to one’s needs.
- Fourth, one may re-evaluate the action based on the outcome (Doya, 2008).
Such normative approaches to decision-making typically assume that the decision-maker has all relevant information available, and all the time in the world to make his decision. Sometimes such models even assume that all possible outcomes of the decision are known beforehand.
In practice, individuals are seldom capable of knowing the possible outcome of the decision with certainty. Many choices involve uncertainty4 or imperfect knowledge about how choices lead to outcomes. Problems raised by decision-making under uncertainty are typically addressed by two separate branches of economics:
- The economics of uncertainty
- The economics of information
The first sees the decisionmaker as accepting the limitations of his knowledge and getting on with making the best decisions he can. The second asks what new information an individual might seek out before making any decisions at all. This means that the economics of uncertainty studies decisions whereas the economics of information studies the preparation for decision-making (Ackert & Deaves, 2010).
As an example, the choice of choosing higher education is indeed associated with uncertainty and risks. Uncertainty of the returns to high education has been identified by Ji (2008) to mainly come from three types of risks.
Firstly, the individual experiences market risks. In a typical dynamic economy frequently exposed to technical and organizational changes along with labor supply shocks etc., the value of human capital and skills often shifts over time. As a result, employees with the same level of education may receive different wages.
Secondly, the individual cannot be certain that he actually is able to complete his education. Thirdly, given the individual’s cognitive ability, the individual also cannot predict precisely what his relative position in the post-education earnings distribution will be. Before going into a deeper analysis of the factors behind human decision-making we will start with the most basic choice theories based on probability theory.
Expected Value Theory
In the seventeenth century, Blaise Pascal recognized that by calculating the likelihood of the different outcomes in a gamble, an informed bettor could choose the option that provided the greatest combination of value and probability. This quantity of value multiplied by probability is now known as “Expected value” (Platt & Huettel, 2008).
In other words, the expected value of a random variable is the weighted average of all possible values that this random variable can take on. The weights used in computing this average correspond to the probabilities in case of a discrete random variable, or densities in case of a continuous random variable. From a mathematical standpoint, the expected value is thus the integral of the random variable with respect to its probability measure.
The expected value may be intuitively understood by the law of large numbers as the expected value is the limit of the sample mean as the sample size grows to infinity. More informally, it can be interpreted as the long-run average of the results of many independent repetitions of an experiment (e.g. a die roll).
The expected value, however, does not exist for some practical distributions with large “tails”, such as the Cauchy distribution (Petruccelli et al., 1999). Furthermore, the expected value may not be expected in the general sense and the expected value itself may be practically unlikely or even impossible, just like the sample mean.
In the case of a one-shot decision as an educational choice, it is worth noting that there is no rule saying that for single-decision problems, one should maximize the expected value. As explained above, the expectation is a way of summarising a distribution of a random variable by a number. It is a simple and intuitive measure, but it does not mean that the only rational thing is to maximize it. Indeed, the expected value is often a poor predictor of people’s choices as variables in practice seldom are identically and independently distributed and the law of large numbers not always applies (Platt & Huettel, 2008).
Expected Utility Theory
In the mid-eighteenth century, Daniel Bernoulli assumed that states of wealth have a specific utility, and proposed that the decision rule for choice under risk is to maximize the expected utility rather than expected value (Kahneman, 2002). He suggested that if one wants to predict human behaviour, one will do better if instead of calculating the expected monetary value of various choices, one calculates the expected value of a utility function of these monetary values (Gilboa, 2010).
The Expected utility theory was further developed by Neumann and Morgenstern in an attempt to define rational behavior when people face uncertainty (Ackert & Deaves, 2010). The theory is normative in the sense that it describes how people should rationally behave5 and Expected utility theory is set up to deal with risk and not uncertainty.
Introducing utility into the weighted sum allows much more freedom, and maximization of expected utility can explain many more phenomena than maximization of expected value. In particular, the choice of education is incompatible with expected value maximization but is in principle compatible with expected utility maximization. Formally, however, it is not clear why people should maximize expected utility rather than some other formula that may or may not involve a utility function.
It is also not necessarily clear whether or not it is reasonable to assume that in reality, people behave as if they had a utility function whose expectation they are seeking to maximize.
The theory of expected utility maximization is more general than expected value maximization, but we may still not be convinced that maximization of expected utility makes sense. An important point, however, is that maximisation of utility does not preclude emotional decision-making. To say that someone maximizes a utility function is merely to say that he is coherent in his choices.
In response to the growing literature on the psychology of decision-making, Akerlof & Kranton (2000 & 2002) were among the first to emphasize the physiological aspects of educational choice by introducing exogenous physiological gains and costs determined by their own social category into a frame of Expected utility theory. Akerlof & Kranton (2002) proposed a utility function that incorporates “identity”6 as a motivation for educational choice-behavior. Identity, associated with a certain social category, defines how people in this category should behave.
They also claim that each social category imposes an “identity” on its members, which creates the relevant psychological and social costs when the individual violates the identity (Ji, 2008). The psychological and social costs are derived from the difference between the agents' own characteristics and the ideal of the assigned category, as well as from the difference between the agents’ educational choice and the educational level in the ideal social category (Akerlof & Kranton, 2000 & 2002).
Based on given utility settings, Akerlof & Kranton (2002) then constructed a game-theoretic model where schools promote a single social category, and the students choose between the “ideal academic identity” and an identity fitting their social backgrounds. When the students hold two contradictory ideas simultaneously, Akerlof & Kranton (2002) term the phenomena as “cognitive dissonance”.
When experiencing such dissonance, individuals have a fundamental cognitive drive to reduce it by modifying the existing belief, or by rejecting one of the contradictory ideas at a physiological cost. An interesting example is when the cognitive dissonance is so large that the psychological costs of keeping an “ideal academic identity” are greater than the benefits of future wages and of an ideal self-image. Akerlof &
Kranton (2002) points out that students from lower social classes are often trapped in such situations, and then end up rejecting the higher educational system.
Although, expected utility models, in general, provide a simple and powerful theoretical framework for choice under risk, and advanced expected utility models, as the one by Akerlof & Kranton (2002), does give indications of why some individuals fail in higher educational achievements, the model, however, does not give any suggestions of how to address and overcome this problem. Decision-problems can be presented in many different ways and Ackert & Deaves (2010) argue that some evidence suggests that people’s decisions are not the same across various presentations. When a choice
problem is presented to a person, a change in the frame can lead to a change in decision. There is numerous evidence of such phenomenon (e.g. Kahneman, 2002, Camerer, 1981 and Tversky & Kahneman 1974). Such framing effects are violations of the expected utility theory, as the theory rests on the assumption that people should have consistent choices regardless of presentation (Ackert & Deaves, 2010). This is presented further in section 2.7.4.
Similarly, across a wide range of economic situations and situations similar to the educational choice, uncertainty leads to systematic violations of expected utility models. As highlighted by Camerer (1981), many real-world decisions have a complex form of uncertainty, because the distribution of outcomes itself is unknown. For example, no one can know in advance all of the consequences that will follow from enrolling at one higher education or another.
When the outcomes of a decision cannot be specified, even with estimated risk probabilities, the decision is said to be made under ambiguity (Platt & Huettel, 2008). Under such circumstances, people are observably even more averse to ambiguity than to risk alone (Forbes, 2009). Such observations have formed the basis for Prospect theory which will be presented in the following section.
The Allais Paradox
Persistent documentation of contradiction of Expected utility theory is the so-called “Allais paradox” suggested by the French economist Maurice Allais in the 1950s. The Allais paradox arises when comparing participants’ choices in two different experiments, each of which consists of a choice between two gambles, A and B. By changing only the likeliness of outcomes, Allais proved that people do not make choices in accordance with certain axioms on which the Expected utility theory rests (Ackert & Deaves, 2010).
The inconsistency stems from the fact that in Expected utility theory equal outcomes added to each of the two choices should have no effect on the relative desirability of one gamble over the other. That is, equal outcomes should “cancel out” (Forbes, 2009). The paradox is an example of how the Expected utility theory seems to be struggling to explain choices under uncertain outcomes.
Such observations encouraged the development of a more descriptive theory of choice such as the Prospect theory as we will look into in section 2.3. Firstly, however, we will return to the homo economicus assumption in a broader market sense expressed in terms of the efficient market hypothesis.
The efficient market hypothesis
According to the efficient market hypothesis, financial prices incorporate all available information and prices can be regarded as optimal estimates of true investment value at all times. The efficient market hypothesis is based on the notion that people behave rationally, maximize expected utility accurately and process all available information. In other words, financial assets are always priced rationally, given what is publicly known.
Stock prices approximately describe random walks through time, i.e. price changes are unpredictable since they occur only in response to genuinely new information, which by the very fact that it is new, is unpredictable. Due to the fact that all information is contained in stock prices, it is impossible to make an above-average profit and beat the market over time without taking excess risk.
Eugene Fama has provided a careful description of an efficient market that has had a lasting influence on practitioners and academics in finance. According to Fama (1965), an efficient market is:
“ ...a market where there are large numbers of rational profit maximisers actively competing, with each trying to predict future market values of individual securities, and where important current information is almost freely available to all participants. In an efficient market, on the average, competition will cause the full effects of new information on intrinsic values to be reflected “instantaneously” in actual prices. A market in which prices always “fully reflect” all available information is called “efficient”.
Notice that the definition of an efficient market relies critically on the information. Fama (1965) defined three versions of market efficiency to clarify what is intended by “all available information“. In the weak form, prices reflect all the information contained in historical returns.
In the semi-strong form, prices reflect all publicly available information, including past earnings and earnings forecasts, everything in the publicly released financial statements (past and most recent), everything relevant appearing in the business press, and anything else considered relevant. In the strong form, prices even reflect information that is not publicly available, such as insiders’ information.
Notice that if prices always reflect all information, we must be assuming that the cost of information acquisition and information generation is zero. Of course, we know that this is not reasonable. Thus, a better working definition of the efficient market hypothesis is that prices reflect all information such that the marginal benefit of acting on the information does not exceed the marginal cost of acquiring the information.
What does market efficiency imply?
In finance and economics, an efficient market is often taken to imply that an asset’s price equals its expected fundamental value. For example, according to the present value model of stock prices, a stock’s price equals the present value of expected future dividends. Price in this specific case is thus simply expressed as:
(2.1)
where pt is the stock price today at time t, Et(dt+i) is the expected value of the future dividend at time t+i using information available today, and δ is the discount rate, which reflects the stock’s risk. Some of the evidence against the efficient market hypothesis discussed later in the book is based on violations of this relationship. Test of the present value model must specify the information available to traders in forming their expectations of future dividends. The present model of stock prices says that, in an efficient market, a stock’s price is based on reasonable expectations of its fundamental value.
Note that market efficiency does not suggest that individuals are ill-advised to invest in stocks. Nor does it suggest that all stocks have the same expected return. The efficient market hypothesis, in essence, says that while an investment manager cannot systematically generate returns above the expected risk-adjusted return, stocks are priced fairly in an efficient market. Because investors have different attitudes toward risk, they may have different portfolios. The efficient market hypothesis, hence, does not suggest that any stock or portfolio is as good as any other.
In addition, while the efficient market hypothesis suggests that excess return opportunities are unpredictable, it does not suggest that price levels are random. Prices are fair valuations of the firm based on the information available to the market concerning the actions of management and the firm’s investment and financing choices.
Behavioural Finance
For a while, theoretical and empirical evidence suggested that the capital asset pricing model, the efficient market hypothesis and other rational financial theories did a respectable job of predicting and explaining certain events. However, as time went on, academics in both finance and economics started to find anomalies and behaviors that couldn’t be explained by theories available at the time. While these theories could explain certain “idealized” events, the real world proved to be a very messy place in which market participants often behaved very unpredictably.
Behavioral finance is an add-on paradigm of finance, which seeks to supplement the standard theories of finance by introducing behavioral aspects to the decision-making process. Contrary to the Markowitz and Sharp approach, behavioral finance deals with individuals and ways of gathering and using information. At its core, behavioral finance analyses the ways that people make financial decisions.
Behavioral finance seeks to understand and predicts systematic financial market implications of psychological decision processes. In addition, it focussed on the application of psychological and economic principles for the improvement of financial decision-making.
Challenging the efficient market hypothesis
Market efficiency, in the sense that market prices reflect fundamental market characteristics and that excess returns on the average are leveled out in the long run, has been challenged by behavioral finance. There have been a number of studies pointing to market anomalies that cannot be explained with the help of standard financial theory, such as abnormal price movements in connection with initial public offerings (IPOs), mergers, stock splits, and spin-offs.
Throughout the 1990s and 2000s, statistical anomalies have continued to appear which suggests that the existing standard finance models are, if not wrong, probably incomplete. Investors have been shown not to react “logically” to new information, but to be overconfident and to alter their choices when given superficial changes in the presentation of investment information.
During the past few years, there has, for example, been media interest in social media stocks, as with Facebook IPO’s recently. Most of the time, as we know in retrospect, there was a positive bias in media assessments, which might have led investors in making incorrect investment decisions.
These anomalies suggest that the underlying principles of rational behavior, underlying the efficient market hypothesis, are not entirely correct and that we need to look, as well, at other models of human behavior, as have been studied in other social sciences. The following sections introduce some of the basic findings and principal theories within behavioral finance that often contradict the basic assumption of standard financial theory.
Prospect theory
The first part of this chapter briefly presented the traditional standard economic approach to understanding individual behavior, financial decision-making, and market outcomes. This subsection will consider more recent attempts to describe behavior that incorporates observed aspects of human psychology.
At the core of behavioral finance is the prospect theory suggested by two psychologists Kahnemann & Tversky in the 1970s. Prospect theory is a mathematically formulated alternative to the theory of expected utility maximization. The expected utility theory offers a representation of truly rational behavior under certainty. According to the expected utility theory, investors are risk-averse.
Risk aversion is equivalent to the concavity of the utility function, i.e. the marginal utility of wealth decreases. Every additional unit of wealth is valued less than the previous equivalent increase in wealth. Despite the obvious attractiveness of the expected utility theory, it has long been known that the theory has systematically failed to predict human behavior, at least in certain circumstances7. Kahnemann & Tversky (1974) found empirically that people underweight outcomes that are merely probable in comparison with outcomes that are obtained with certainty; also that people generally discard components that are shared by all prospects under consideration. Under prospect theory, value is assigned to gains and losses rather than to final assets. Also, probabilities are replaced by decision weights.
Another foundation of the prospect theory is the value function (see figure 1). The value function differs from the utility function in expected utility theory due to a reference point, which is determined by the subjective impression of individuals.
According to the conventional expected utility theory, the utility function is concave downward for all levels of wealth. On the contrary, according to the value function, the slope of the utility function is upward sloping for wealth levels under the reference point and downward sloping for wealth levels after the reference point. The reference point is determined by each individual as a point of comparison, e.g. a measure of a target level of wealth.
For wealth levels under this reference point, investors are risk seekers, i.e. they are prepared to make riskier bets in order to stay above their preferred target of wealth. Whereas for wealth levels above this reference point, the value function is downward sloping, in line with conventional theories, and investors here are risk-averse. Kahnemann & Tversky (1974) asserted that people are risk seekers for losses.
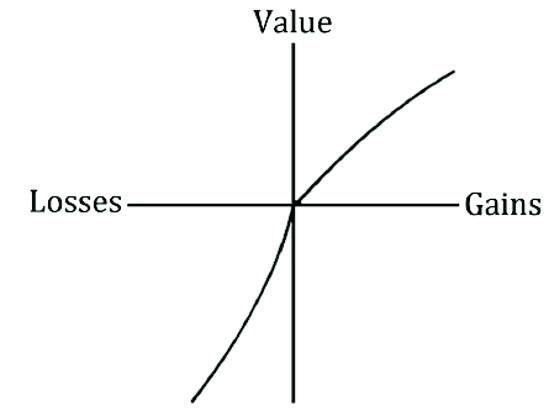
Figure 1: Kahnemann & Tversky’s Value Function (Based on Kahnemann & Tversky, 1974)
The two phenomena observed by Kahnemann & Tversky (1974), the preference for certain outcomes and the preference for risk when faced with losses, may explain some premises of investors’ irrational behavior.
Due to the fact that the reference point in the value function always moves with wealth to stay at the perceived current level of utility, investors will always behave in a risk-averse manner even when small amounts of wealth are in question (people are risk-seeking in losses, but risk-averse in gains). Subsequently, they will always prefer taking a risk when confronted with losses.
This phenomenon, called “loss aversion”, is presented briefly in the following subsection. Likewise, regret is an aspect of the prospect theory that can be traced to the value function theory.
Like many theories, prospect theory has changed since its original form. While in the original version of prospect theory published in 1979 Kahnemann & Tversky spoke of what conditions an appropriate weighting function should embody, they did not attempt to formulate such a function.
This was left to their more mathematically rigorous version of prospect theory, known as “cumulative prospect theory”. Cumulative prospect theory answers some technical objections to the original theory (for example that prospect theory originally violated statistical dominance). In this book, only graphical illustrations of the value function (see figure 1) and the weighting function (see figure 2) are presented.
Cumulative prospect theory has been used to explain the “equity premium puzzle” (why stocks enjoy such high returns compared to bonds) and various stock market anomalies as is presented in chapter 4.
Loss aversion
Prospect theory supposes that people’s utility derives from losses and gains, rather than from final wealth. People work from a psychological reference point and strongly prefer to avoid losses below it. The value function shows the sharp asymmetry between the values that people put on gains and losses. This asymmetry is called “loss aversion”.
Empirical tests indicate that losses are weighted about twice as heavily as gains, i.e. losing 1€ is about twice as painful as the pleasure of gaining 1€. This can also be expressed as the phenomenon in which people will tend to gamble in losses, i.e. investors will tend to hold on to losing positions in the hope that prices will eventually recover. This is due to the fact that the utility function under the prospect theory is upward sloping for wealth levels under each individual’s reference point.
Loss aversion can help to explain the tendency of investors to hold on to loss-making stocks while selling winning stocks too early. Shefrin (2000) called this occurrence the “disposition effect”. This hypothesis has been supported empirically for field data (Heisler, 1994; Odean, 1998), and in experimental asset markets (Heilmann et al., 2000; Weber & Camerer, 1998). Odean (1998) analyzed trading records for 10,000 accounts at a large discount brokerage house and found that investors held losing stocks for a median of 124 days, while winners were held for only 104 days.
Using an experimental call market, Heilmann et al. (2000) showed that the number of assets offered and sold was higher during periods of rising trading prices than during periods of falling trading prices. When investors view stocks on an individual basis, then risk aversion in gains will cause them to sell too quickly into rising stock prices, thereby depressing prices relative to fundamental values.
Conversely, risk-seeking in losses will cause investors to hold on too long when prices decline, thereby causing the prices of stocks with negative momentum to overstate fundamental values. Loss aversion also implies that decision-making is sensitive to the description of the action choices, i.e. to the way the alternatives are “framed”. This important role of frames is presented in the following section.
Framing and mental accounting
Framing and mental accounting are both parts of the prospect theory. A decision frame is a decisionmakers view of a problem and the possible outcomes. A frame is affected by the presentation, the person’s perception of the question, and personal characteristics. If a person’s decision changes simply because of a change in the frame, expected utility theory is violated because it assumes that people should have consistent choices, regardless of presentation.
Mental accounting describes the tendency of people to place particular events into different mental accounts, based on superficial attributes. The main underlying idea is that decision-makers tend to separate the different types of gambles they face into separate accounts, and then apply prospect theoretic decision rules to each account, thereby ignoring possible interaction between the accounts. Mental accounts can be isolated not only by content but also with respect to time. The mental accounting bias also enters into investing.
For example, some investors divide their investments between a safe investment portfolio and a speculative portfolio in order to prevent the negative returns that speculative investments may have from affecting the entire portfolio. The problem with such a practice is that despite all the work and money that the investor spends to separate the portfolio, the investor’s net wealth will be no different than if he had held one larger portfolio. Mental accounting can serve to explain why investors are likely to refrain from readjusting his or her reference
point for a stock. When the stock is purchased, a new mental account for the particular stock is opened. The natural reference point, as in the Kahnemann & Tversky valuation function described in previous subsection, is the asset purchase price. A running score is then kept on this account indicating gains or losses relative to the purchase price.
When another stock is purchased, another separate account is created. A normative frame recognizes that there is no substantive difference between the returns distributions of the two stocks, the only difference in names. However, a situation involving the sale of the first stock when it has decreased in price and using the proceeds to buy the second stock may be framed as closing the first stock account at a loss. It has been argued that decision-makers encounter considerable difficulty in closing a mental account at such a loss.
The role of frames is also illustrated in the dividend puzzle according to which private investors treat dividends separately from capital gains. In a world without taxes and transaction costs, investors should be indifferent between a dividend Euro and a capital Euro.
Moreover, in a world where dividends are taxed more heavily than capital gains, standard investors know that they are actually better off when companies refrain from paying dividends. So why do companies pay dividends? A dividend Euro is different from a capital Euro according to the prospect theory because the investor frames the Eurosinto two distinct mental accounts. Therefore, even though a stock paying out dividends might be decreasing in price an investor may be reluctant to sell the stock in fear of closing a mental account containing dividend income.
Dividends can be thought of as a separate gain from capital gain due to the rise in the stock price itself. Financing consumption out of dividends further avoids the anticipated regret of selling a stock that might later rise in value.
One could argue that private investors think naturally in terms of having a “safe” part of their portfolio that is protected from downside risk and a risky part that is designed for getting rich. Mental accounting can also result in “good money being thrown after bad money” by a continuous operation of non-profitable ventures in the hope that recovery will somehow take place. It may also explain framing which is beneficial to investors with imperfect self-control. Glick (1957) reports that the reluctance to realize losses constitutes a self-control problem.
He describes professional traders who are very prone to let their losses “ride”. It is the control of losses that constitutes the essential problem. The traders’ problem was to exhibit sufficient self-control to close accounts at a loss even though they were clearly aware that riding losses was not rational. Self-control is also exhibited in the dividends puzzle, mentioned above.
For example, old investors, especially retirees who finance their living expenditures from their portfolios, worry about spending their wealth too quickly, thereby outliving their assets. They fear a loss of self-control, where the urge for immediate gratification can lead to overspending.
Integration versus segregation
In many cases, the decision-maker chooses a reference point, and whether an outcome is perceived as positive or negative will depend on the reference point selected. For example, as adapted from Tversky & Kahnemann (1981), suppose you lost 150€ at the horse track today. You are considering betting another 10€ in the next and final race of the day on a horse with 15:1 odds.
This means that if your horse wins, your payoff for the race will be 150€, but if your horse loses, you lose the 10€ bet. Notice how important the bettor’s reference point is here. If he includes his losses over the day, the bet
will result in either a break-even position if the horse wins or an overall loss of 150€ if the horse loses (plus the 10€ lost in the final race). But if the bettor ignores his prior losses and considers his reference point to be a fresh slate, the outcome of the final bet is either a gain of 150€ or a loss of 10€.
Prospect theory predicts that a decision-maker who adopts the latter approach of segregating outcomes will be less inclined to accept risk in this situation, both because the gamble crosses over between loss and again so that loss aversion stares at the decision-maker, and, to the extent that we are in the domain of gains, the value function is concave. In contrast, a decision-maker who takes the first reference point and integrates the outcomes of the bets on the day will be more risk-seeking since this decision-maker will be in the domain of losses.
Integration occurs when positions are lumped together, while segregation occurs when situations are viewed one at a time. Standard prospect theory mostly assumes that people segregate, though Kahnemann & Tversky (1981) did recognize that sometimes people adopt the frame of integration. They note, for example, that more bets are placed on long shots at the end of the racing day, suggesting that a least some bettors are integrating the outcomes of races and taking risks they would not ordinarily take in order to try to break even.
In the horse racing example, some people are willing to increase their risk in order to break even. When risk increases after losses, this is called the “break-even effect”. How would people behave, according to the prospect theory, after gains? Symmetry might suggest that risk-taking would decline, but the reality is otherwise. If new decisions (e.g. whether and how much to bet on the next race) are integrated with prior gains, then, because you have moved up the value function and are some distance from the loss boundary, it is likely that you will be willing to assume greater risk.
Using the language of the casino rather than from the track, you are betting with the “house money”. The “house money effect” is said to be operative when someone increases risk-taking after prior gains. Both the break-even effect and the house money effect are quite important in the context of financial decision-making because they may influence decisions after portfolio growth or shrinkage. We will look more into this in section 3.5.1. At first, however, we will introduce the theories behind heuristics and biases.