Monopoly
- Details
- Category: Microeconomics
- Hits: 9,108
A monopoly can be viewed as the opposite of perfect competition. Instead of many firms, there is only one: the monopolist. This has important consequences for both price setting and the quantity produced.
Barriers to Entry
Why do monopolies arise? There are many different reasons, but all of them have to do with barriers to entry in the market. The reasons for these barriers could be structural. There are properties of the market that automatically shut competitors out:
- Economies of scale. If there are economies of scale, large-scale advantages, the size of the firm is crucial for the average cost. A situation can then arise in which only one firm can recover its costs. This is called a natural monopoly and an example of this is railroads.
- Cost advantages. If the monopolist has access to a cheaper way of producing the good, for instance, if she has a patent on a cheaper technology, she can push competitors out of the market.
- Strategic limitations. The monopolist can create barriers to entry. An example is limit pricing, where the monopolist sets the price so low that it becomes unattractive for competitors to enter.
- Political. The government may decide to grant a firm a monopoly in a certain market. A common example is for pharmaceutical goods.
- Patents and exclusive rights. If a firm has a patent on a certain good, other firms are shut out during the life span of the patent. It is also possible to have the exclusive right to extract, for instance, oil or metals.
Demand and Marginal Revenue
In this chapter, we will assume that the monopolist charges all customers the same price. The monopolist faces the whole demand of the market. We can compare it with a perfectly competitive market by looking again at Figure 9.2.
The individual firm in a competitive market only faces a small part of the market. Therefore, it can be represented on the right-hand side of the figure. A monopolist is a whole market. Therefore, it looks like the left-hand side of the figure. In order to sell more goods, the monopolist has do reduce the price, and the demand curve it faces will, therefore, slope downwards.
Now, note that the demand curve is decided by the consumers and not by the firm. It answers the question: if we would offer a certain price, how many units would we then be able to sell? In a perfectly competitive market, marginal revenue was equal to the price.
That is not the case for a monopolist. For the monopolist to be able to sell an additional unit of the good, she must lower the price of all units. The total effect of selling one more unit then consists of both what she is paid for the last unit and of the reduction of revenue from all the other units that she now has to sell at the lower price. Consequently, the marginal revenue will be lower than the price.
Let us see what this means for a good with linear demand. If the demand curve is a straight line, the MR curve will also be a straight line with the same intercept on the Y-axis as the demand curve. However, it will have a slope with twice the magnitude. (To show that, we need to use the derivative, but this, again, is outside the scope of this book.)
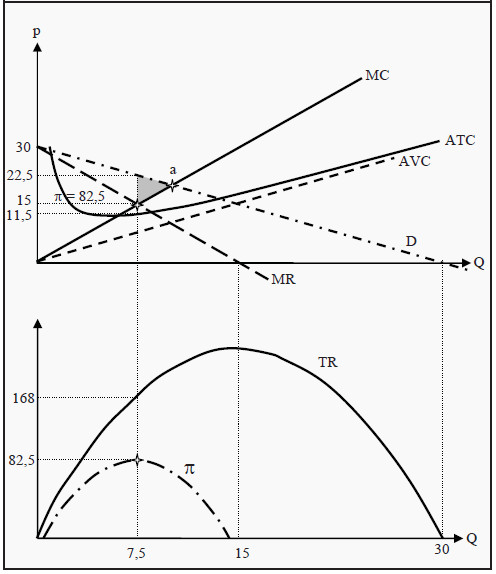
Figure 11.1: The Profit Maximum for a Monopoly
We will use the demand curve QD = 30 - p, or if we solve for p: p = 30 – QD (see Section: How to Find the Equilibrium Point Mathematically). If the MR curve is to start at the same point and have a slope that is twice as large, its functional form must be MR = 30 - 2* QD. (The constant is the same, 30, and the slope is changed from -1 to -2). In Figure 11.1 the curves are drawn as D and MR. We have also drawn a marginal cost curve, MC (= 2*Q), an average cost curve, ATC, and an average variable cost curve, AVC (= Q), and, in the lower part of the figure, total revenue, TR, and profit, π.
Profit Maximum
The monopolist wants to maximize her profit. She does that by producing the quantity, Q*, at which MC = MR:
MC (Q*) = MR (Q*)
In Figure 11.1, this corresponds to the quantity 7.5, where both MR and MC equal 15. To see that this choice maximizes the profit, think of what would happen if she would produce more than that quantity. If she would produce one more unit, she would get paid MR but also incur a cost of MC. Moreover, since MC > MR, the cost is larger than the revenue and she would reduce profit; similarly, if she would reduce the production.
The profit at a quantity of 7.5 is, according to the lower diagram, 82.5. The price the monopolist will charge is the one that the consumers, according to the demand curve, are prepared to pay when the total production is 7.5, i.e. 22.50.
The corresponding ATC is 11.50. In other words, the monopolist makes 22.50 - 11.50 = 11 per unit sold, totaling to 11*7.5 = 82.5. This corresponds to the grey rectangle in the upper part of the figure.
Similarly to the firms in a perfectly competitive market, the price must also be above the average variable cost, AVC. If it is not, it is better to produce nothing at all. In the long run, the firm must also cover its fixed cost, and then the price must be above the average total cost, ATC.
In Figure 11.1, we have also indicated where total revenue is maximized. This occurs at the quantity Q = 15 and corresponds to the point in the upper part of the Figure where MR = 0. Note that this point does not maximize profit. In the example, the firm makes a loss at that quantity.
The Deadweight Loss of a Monopoly
To have a monopoly firm is often very beneficial for the monopolist, who can make a profit, but it is negative for society. To see why to look at point an in the upper part of Figure 11.1. In that point MC = D. The marginal cost is the cost of the last produced unit, and the demand is the consumers’ corresponding valuation of that unit.
At point a, the cost of producing the last unit and the valuation of that unit is the same. To the left of that point, the consumers’ valuation is higher than the cost of producing additional units. Society, therefore, loses the production of goods that cost less than what they are worth, according to the consumers’ valuation. Then the quantity that the monopolist produces cannot be efficient. The deadweight loss that arises corresponds to the dark grey triangle in the figure.
Let us look closer at the consequences. In Figure 11.2, we have drawn the supply curve, i.e. the MC curve. (Remember that the supply curve of a firm corresponds to the part of the MC curve that is above the average cost.) Furthermore, we have drawn the demand curve, D, and the marginal revenue curve, MR.
Under perfect competition, equilibrium had been reached at the price PC and the quantity QC, but in a monopoly market, equilibrium is reached at the price pM and the quantity QM. The producer surplus (PS) in a monopoly market corresponds to the area B + D, and the consumer surplus (CS) corresponds to the area A. The social surplus will, therefore, be A + B + D.
If the market had been perfectly competitive instead, PS had been D + E while CS had been A + B + C and the social surplus A + B + C + D + E.
In other words, society, particularly the consumers, loses utility: The deadweight loss is C + E. The monopolist, on the other hand, will lose if the competition is increased. Note that the monopoly is not efficient (see Section 18.2): It would have been possible to produce the quantity QC to the price PC and then compensate the firm by transferring the area B back from the consumers.
The consumers would still get an increase in utility corresponding to the area C (they would now get A + C), and the producers would get an increase in utility corresponding to the area E (they would now get B + D + E). No group would lose anything. Therefore, the monopoly does not fulfill the Pareto criterion.
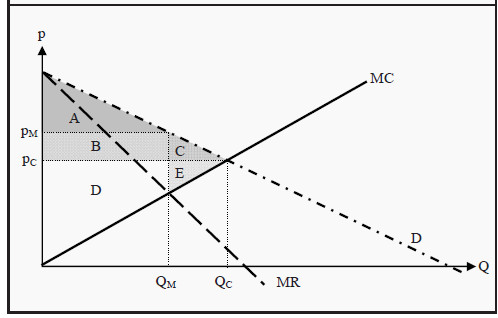
Figure 11.2: Deadweight Loss of a Monopoly
Ways to Reduce Market Power
To reduce the negative impact on society, governments often try to limit the market power of monopolists. Some popular measures include
- Price regulations. If it can be known what the market price would have been under perfect competition, or if the cost of production is known, the government can decide on a price ceiling at that price. Thereby, the equilibrium point is moved to the optimal point from society’s viewpoint. It is, however, very difficult to estimate the optimal price.
- Increase competition. If the monopoly has been created through political decisions, the regulation can be changed.
Price Discrimination
There are more possibilities for a monopolist to take advantage of her situation: She can charge different prices from different customers. This is called price discrimination, and we distinguish between price discrimination of the first, second, and third degrees.
First Degree Price Discrimination
Remember that the demand curve corresponds to the consumers’ valuation of different quantities of the good. Suppose, for example, that we have four presumptive consumers who want to buy a maximum of one unit of the good. The first is willing to pay 4 for one unit of the good, the others 3, 2, and 1, respectively.
We then get a demand curve as D in Figure 12.1: If the price is 4, we sell one unit to the first customer, if it is 3 we sell one unit to each of the first two, and so on. We have indicated the reservation prices of each customer with a star and then joint them with a straight line.
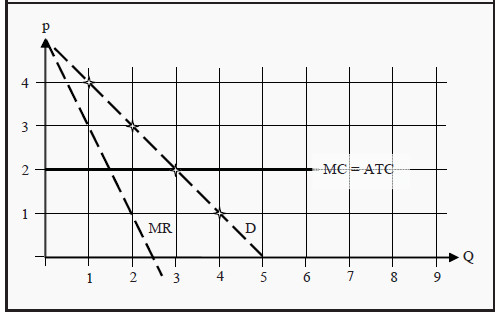
Figure 12.1: First Degree Price Discrimination
Furthermore, assume that the monopolist has a constant marginal cost MC = 2, and no fixed cost. Then AVC = ATC = MC. In a perfectly competitive market, the equilibrium price would have been p* = 2 and the quantity sold would have been Q* = 3. The firm’s revenue would have been 3*2 = 6 (Q*p), and its cost 3*2 = 6 (Q*ATC). Its profit would therefore have been zero.
The consumer surplus (CS) would have been the sum of each customer’s surplus, i.e. the difference between his or her valuation and how much he or she pays. For the first customer, the surplus is 4 - 2 = 2, for the second 3 - 2 = 1, and for the third 2 - 2 = 0. Therefore, we get a total consumer surplus of CS = 3.
In a monopoly market of the type we analyzed in this post, the firm would have found the quantity at which MC = MR, i.e.Q = 1.5. If it can only sell whole units, it would have chosen to produce only one unit that it would have sold at a price of 4. The profit (= PS) would then be 1*(4 - 2) = 2, which is higher than in the perfectly competitive case. CS would be 4 - 4 = 0.
Suppose now instead of that the monopolist knows the valuation of each consumer, and that the consumers cannot sell the goods to someone else if they have bought it. The monopolist can then use price discrimination of the first degree (also called perfect price discrimination): She charges a price from each customer that is equal to the maximum amount that the customer is willing to pay.
The first customer has to pay 4, the second 3, and the third 2. Since the monopolist has a marginal cost of production equal to 2, her surplus will be PS = (4 - 2) + (3 - 2) + (2 - 2) = 3. CS will be 0. Compared to a perfectly competitive market, the monopolist has won over all the CS.
Note that in this case, with first-degree price discrimination, the social surplus is as just large as in the case of perfect competition. The surplus has just been reallocated from the consumers to the producers. This means that this situation is actually efficient. It is another question whether it is fair.
Second Degree Price Discrimination
If the monopolist does not know the different valuations of different customers, she can instead use second-degree price discrimination. This amounts to offering different package solutions at different prices, and then the customers get to choose which package they prefer.
By choosing the composition of the packages in a clever way, she can get the customers to sort themselves into different groups. The goal of making them perform this type of self-sorting is to get the ones with high valuation to pay a high price and the ones with low valuation a lower price. An example of this type of price discrimination is quantity discounts.
Third-Degree Price Discrimination
The third type of price discrimination amounts to dividing the market into two or more submarkets, where the valuations in the submarkets are different. Examples are different prices for children and grownups, or discounts for students and the unemployed. For this to work, it has to be possible to identify the consumer as actually belonging to a certain group.
The criterion for profit maximization under third-degree price discrimination is, in principle, the same as before, but we have to separate demand and marginal revenue in the two (or more) submarkets. Mathematically, this can be written as
MC(Q1 +Q2 ) = MR1(Q1) = MR2( Q2)
In other words, the marginal cost of producing the total quantity has to be as large as the marginal revenue from the first submarket, and simultaneously as large as the marginal revenue from the second submarket. With constant MC and linear demand in both submarkets, this can be illustrated as in Figure 12.2.
The firm chooses to produce the quantity Q1 + Q2, and then sell the quantity Q1 at a price of p1 in the first submarket and the quantity Q2 at a price of p2 in the second submarket.
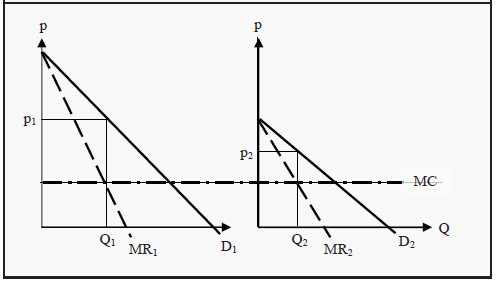
Figure 12.2: Third Degree Price Discrimination