Prices and inflation

Prices and price level

Price level

Prices are of great importance in macroeconomics as indeed they are in microeconomics. However, in microeconomics we are more interested in prices of individual goods and services and such prices are rarely important for the economy as a whole although there are exceptions (for example, the price of oil).

In macroeconomics, we are more interested in how prices change on average. We define the price level as a weighted average of several different prices. If p₁ is the price of gasoline and p₂ the price of oil, then 10 p₁ + p₂ is a price level. It is a weighted average of two prices with weights 10 and 1. Normally, the price level is defined using many more prices.

The reason for using different weights is that some prices are more important than others for the economy. The price of gasoline, for example, is much more important than the price of paper clips. By using different weights we allow for changes in some prices to have a larger effect on the price level than changes in other prices.

Exactly which prices are included in the price level and the weights they carry may vary. Different choices give rise to different measures of the price level. To visualize the prices and weights that are included, we use the concept “basket” of goods and services.

We may, for example, create a basket that contains all the goods sold by a particular store on a particular day. The price of this basket is then a price level – it will be a weighted average of the prices of the goods sold that day and the weights will be equal to the number of each good sold. Perhaps the basket contains 100 liters of regular milk but only one frozen cake.

The price of regular milk will then have a weight of 100 while the price of frozen cake will have a weight of 1. Changes in the price of milk will then have a greater influence on the price level than changes in the price of the frozen cake.

Note: in macroeconomics, it is common to use the term “prices” or “price” as short for the price level. The expression “prices rise” should be interpreted as “the price level rises” – it does not mean that all prices rise.

Price level and time

We are rarely interested in the value of the price level at a particular point in time. What we are interested in is the percentage change in the price level between two points in time. We calculate the percentage change by first creating a basket of goods and services. At regular intervals (usually once a month on the first day of the month) we measure all the prices of the contents of the basket (typically as an average of the market) and calculate the price level. In this way, we will end up with a time series of price levels – one value for each month.

Using this time series we can study how the price level evolves over time. If all prices rose by 2% during one month, the price level would rise by exactly 2%. If one of the prices rose by 2% while the other prices remained unchanged, the price level would rise, but by much less than 2%. Exactly how much it would raise would depend on the weight of the changed price.

Imagine that we have created a particular basket of goods and services. We calculate the price level at four different points in time during 2008 without changing the content of the basket (the weights are unchanged). Suppose that we find the following time series for the price level :

Price index

Since we are only interested in the percentage change of the price level and not the particular value, we can divide each price level by a given constant so that the numbers are easier to deal with. When we divide a series of price levels by a constant we end up with what is called a time series of price indexes. Using the same basket as above, if we divide the entire series by 607.70 we get the following time series of price indexes:

The reason for choosing 607.70 is that we want the index to be equal to 100 for the first point in time. The advantage of having an index that starts with 100 is that we will have a clearer picture of the evolution of prices. We may, for example, immediately conclude that prices rose by 2.68% on average in January and by 3.42% during the three months from January to March.

Note that the percentage change of the original price level and the percentage change of the price index is the same. The percentage change will not depend on which point in time we select as our “base” (giving the price index value of 100). Using the price index, the percentage change during January is (62400 – 60770)/60770 = 2,68% which is exactly the same as the percentage change of the price index.

Consumer Price Index (CPI)

Consumer Price Index (CPI)  is a price index of a particular basket called the CPI-basket. The CPI-basket contains basically all the goods and service consumed in a country – food, gas, medicine, haircuts, transportation, house rent and so on. The composition of the CPI basket is determined by the value of what is consumed in the country – the larger the value of total consumption of a good or service, the larger the weight in the basket.

For example, if we spend twice as much on apples as on pears, apples will have twice the weight in the basket. The exact details of the composition of the basket and how the Consumer Price Index (CPI)  is calculated are complicated and vary somewhat between countries. Figure 1 displays CPI for Germany after the reunification starting at January 1991. This data has 2005 as the reference year. This means that the CPI is constructed in such a way that CPI is exactly equal to 100 on average during 2005.

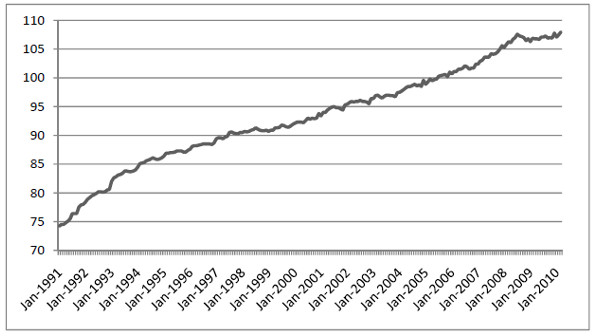
Figure 1.1 Consumer price index (CPI) for Germany 1991 – 2010. Source: OECD.

Problems with Consumer Price Index (CPI)

To illustrate the problems involved in calculating the CPI we consider MP3 players. If you measure the average price of MP3 players at two points in time, say one year apart, you may find that the average price has not changed.

However, this is not the whole story since the products on the market will have changed. Typically, the products at the later measurement are more advanced than the products at the first measurement. If you were to compare the prices of MP3 players with the same performance, you would probably find that prices have fallen. Without adjusting for changes in performance and quality, you will usually overestimate the rise in the price index.

Inflation

The inflation between two points in time is defined as the percentage increase of the price index between these two points in time. Comments:

• The price index is calculated at a particular point in time, inflation over a time period, typically one year
• Inflation may just as well be defined as the percentage change in the price level.
• Inflation is independent of which year we use as our base year for our price index.
• You often hear that inflation is the “percentage change in prices” but keep in mind that “prices” are then short for the price level.
• Since the price level may be defined in many different ways (using different goods and different weights in the basket), inflation may be defined in many different ways.
• If the price index decreases between two points in time we say that inflation is negative or that we have deflation.

Inflation in Germany

Once we have monthly data on a price index we can calculate the inflation. In most countries, the percentage change in the price index during one month is small. Therefore, it is more common to calculate the inflation each month based on an entire year.

For example, on 1 January 2010, inflation is calculated as the percentage change in the price index between 1 January 2010 and 1 January 2010. On 1 February 2010, inflation is calculated as the percentage change in price index between 1 February 2010 and 1 February 2010 and so on. Figure 1.2 shows Germany as an example.

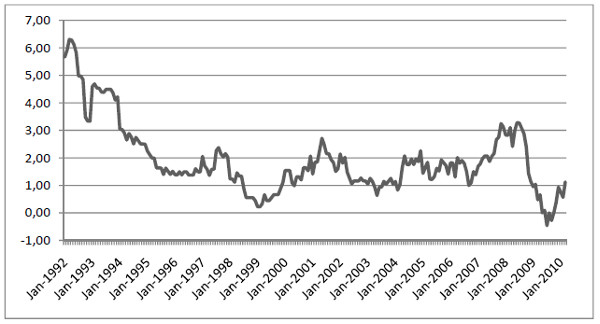
Figure 1.2 Inflation in Germany 1992 – 2010. Source: OECD.

Inflation in Sweden

Figure 1.3 Inflation in Sweden 1830 – 2010. Source: SCB.

Four aspects are interesting when we look at inflation data for Sweden

• During the 1800s, when Sweden was mainly an agricultural society, deflation where almost as common as inflation.

• The “spikes” in 1918-1922 began with a speculative boom right at the end of World War I, which in turn was followed by a deep depression.

• In the period from the end of the Second World War 1945 to the economic crisis of the 1990s, Sweden had continuous inflation with no periods of deflation. Inflation was particularly high during the 1970s and the 1980s.

• From 1992 onwards Sweden has had a low and a relatively constant rate of inflation with regular periods of deflation. A major reason for the low inflation in Sweden, as for most OECD countries, is the priority given to combating inflation. Sweden now has an inflation target aiming to keep inflation to between 1% and 3%.