Game Theory
- Details
- Category: Microeconomics
- Hits: 7,351
Before we go on to the other market forms, oligopoly and monopolistic competition, we will introduce a tool called game theory. Game theory is a much younger tool than most of the others we have discussed so far and has become a large field of research. Here, we will just present two different games.
These will get to represent the two different groups of games: normal form games and extensive form games. We will later use these tools in the analysis of oligopolies.
The Basics of Game Theory
Game theory is used for analyzing how individual agents interact with each other. Depending on the structure, they may take into account how the other agents are choosing (or how they believe that they will choose), and then decide on their own strategy.
This closely resembles the situation in many parlor games. Think, for instance, how the players act in chess: They only decide on their own moves, but they do so depending on how they believe that the opponent will respond. It is most often a bad strategy to hope that the opponent will not discover a trap. A better strategy is to assume that the opponent understands everything that one understands oneself and then base one’s strategy on that.
To turn this into a theory, we need to first define the basic building blocks. For a game to be a game in the relevant sense, we need players, rules, outcomes, and preferences over the outcomes. With chess, the players are “white” and “black,” the rules are the rules for chess, the usual outcomes are “white takes black’s king,” “black takes white’s king” or “draw.” The players’ preferences are usually that they prefer that they take the opponent’s king to a draw, and lastly that the opponent takes their king.
In most games of game theory, we need to specify:
- The players. It could be individuals, firms, or countries. Often, there are only two or three players.
- Actions. All possible actions the different players can choose to do, for instance, decide on quantity or price.
- Information. What each player knows at different stages of the game.
- Strategies. A strategy is a complete description of what a player will choose at each possible situation that could arise in a game. One can think of a strategy as a list. The list should be so exhaustive that another person could play instead of the player, and never actually have to decide anything by herself.
- Payoffs. The utility a player gets, given a certain outcome of the game.
The Prisoner's Dilemma
The game called The Prisoner's Dilemma is probably the most well-known example of game theory. It is also an example of a normal form game (or strategic form game), which means that the players choose simultaneously. (Formally, a normal form game is a game that can be defined by only specifying the players, the strategies, and the payoffs.)
One way to construct the game is the following. Two players, A and B, have been arrested (somewhere where the rule of law is somewhat substandard) and are kept in isolation. A prosecutor suggests A the following:
- If you confess and B does not, you will be set free as a sign of our gratitude. B will then get 10 years in prison.
- If both of you confess, you each get 2 years in prison.
- If B confesses and you do not, you get 10 years in prison while B is set free.
- If none of you confesses, we will frame you for a petty crime and you will each have to pay a small fine.
At the same time, B gets the same suggestion. The two players cannot communicate with each other and therefore must consider a solution in solitude. Let us now identify the different elements that make this a game, in the game-theoretical sense of the word.
- The players; Individuals A and B.
- Actions; For A: choose "Confess" or "Do not confess"; and similarly for B: choose "Confess" or "Do not confess.”
- Information; Both A and B know that the other has received the same offer, but they do not know how the other chooses.
- Strategies. Both A and B can only choose one of two different actions. Possible strategies for A are then "choose confess" or "choose not to confess", and similarly for B.
- Payoffs; Here we need to know the two players’ preferences. For simplicity, we assume that they have the same preferences and that they are as follows: 10 years in prison (-10), 2 years in prison (-2), a small
- fine (-1), and freedom (+1).
Many normal form games can be represented with a so-called payoff matrix, where one player’s strategies are displayed in the vertical direction and the other’s strategies in the horizontal direction. Their respective payoffs that correspond to certain strategy pair are then indicated in the squares. If we do this for the present game, we get the payoff matrix in Figure 13.1. Note that player A’s payoffs are to the left in the squares and player B’s are to the right.
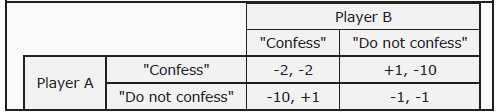
Figure 13.1: Payoff Matrix for the Prisoner’s Dilemma
Let us first look at the game from the perspective of player A. She does not know how player B will choose, but she does know that player B will choose either “Confess” or “Do not confess.” Say that player B would choose “Do not confess.” Then, obviously, the best thing player A can do is to choose “Confess,” since she will then get a utility of +1 (freedom) instead of -1 (a small fine). Now, say that player B chooses “Confess” instead.
Then the best thing player A can do is still to choose “Confess,” since she will then get a utility of -2 (2 years in prison) instead of -10 (10 years in prison). Consequently, player A has a strategy that is the best one, independently of what player B chooses. Such a strategy is called a dominant strategy.
Player B’s problem is the same as player A’s, and hence it is a dominant strategy for player B as well to choose “Confess.” As a result, they both choose “Confess” and get two years in prison. This is so, even though it is possible for them both to get away with a small fine (if they both choose “Do not confess”).
This is the dilemma. For both player A and B it is individually rational to confess, but acting that way they achieve an outcome worse than what is “collectively” possible. If they had been able to cooperate, they would have been able to reach a higher utility level.
Games that have properties such as this one are called Prisoner’s Dilemma games. It could just as well be two countries deciding on whether to wage war on each other, two firms deciding on whether to start a price war or not, or two fishers deciding on whether to restrict their fishing or take the risk that the fish will go extinct. The players are kept from a rather good solution because they choose their own individual best.
Nash Equilibrium
In the last section, we presented a solution to the Prisoner’s Dilemma. With “solution”, we here mean a prediction of how the players will play. How does one generally solve a game? This is far from self-evident, and in many games, there are several different reasonable solutions. The most popular concept for solving games is the Nash equilibrium. There are, however, several other ways in which to solve games, but most often, they are variations of a Nash equilibrium. Note also that, there can be more than one Nash equilibrium in a game.
A Nash equilibrium is:
- A set of strategies, one for each player.
- The strategies should be such that no player can improve her utility by unilaterally changing her own strategy.
Finding the Nash Equilibrium in a Game in Matrix Form
It is often easy to find the Nash equilibrium for a game in matrix form. Look at the game in Figure 13.1 again. We have four squares in the matrix. We can then find the Nash equilibrium by checking each square separately:
- Do not confess, Do not confess1, i.e. the lower right square. Can any of the players improve her situation by unilaterally changing her own strategy? If, for instance, A changes to "Confess" she will get +1 instead of -1. (Similarly for B.) Consequently, she can improve her situation and this cannot be a Nash equilibrium.
- Do not confess, Confess, i.e. the lower left square. If A changes to "Confess”, she will get -2 instead of -10. Consequently, this cannot be a Nash equilibrium either.
- Confess, Do not confess, i.e. the upper right square. If B changes to "Confess”, she will get -2 instead of -10. Consequently, this cannot be a Nash equilibrium.
- Confess, Confess, i.e. the upper left square. If A would change to "Do not confess”, she would reduce her utility from -2 to -10, and if B would change she would also reduce her utility from -2 to -10. None of the players can, therefore, improve on her situation by unilaterally changing her strategy, and this must be a Nash equilibrium. The only Nash equilibrium in the Prisoner’s Dilemma is that both players choose “Confess.”
A Monopoly with No Barriers to Entry
We will now describe a game on the so-called extensive form, where the question is whether a monopolist can uphold her monopoly if there are no barriers to entry.
In a game on the extensive form, there is, in contrast to games on the normal form, an order to the choices. One could say that we have added a time dimension. There are two firms, The Incumbent (J) and the Entrant (E). J has, at the beginning, a monopoly in the market and E has to choose whether to enter the market or not. If she decides to enter it, J can choose to start a price war, i.e. lower the price to punish E, or to accept the competitor. The problem with a price war is that it also hurts J herself.
- The players; The Incumbent (J) and the Entrant (E).
- Actions; For E: choose "enter" or "not enter"; for J: choose "price war" or "accept.”
- Information; E knows what the game structure looks like, but not how J will decide later on. J, on the contrary, knows how E has chosen when it is her time to choose. J consequently has more information than E.
Strategies. For E there are two strategies:
- Choose "enter.”
- Choose "not enter.”
- For J, there are also two strategies:
- Choose "price war.”
- Choose "accept.”
Payoffs. Here we need to know the players’ preferences. Assume these are as in Figure 13.2.
This type of game is usually represented with a so-called game tree. The present game will look like in Figure 13.2.
In the game tree, we have indicated where E and J decide, and what they can decide between at that point. At the far bottom, there are two rows of numbers. The number in the first row indicates the first player’s (E’s) payoff and the number in the second row the second player’s (J’s).
The game tree is read from top to bottom. It begins with E choosing between “not enter” and “enter.” If the she chooses “not enter,” the game ends and E gets 50 while J gets 100. If E, instead, chooses “enter,” J gets to choose between “price war” and “accept.” If she chooses “price war,” the game ends and E gets 25 and J gets 50. Compared to the case when E chooses not to enter, both E and J get a lower payoff. If J, instead, chooses “accept,” the game ends with E and J sharing the market and both getting a payoff of 75.
It is clear that J prefers that E does not enter the market (which gives J 100) to accepting (75), and both of these to a price war (50). E prefers to be accepted (75) to not entering (50), and both of these to a price war (25).
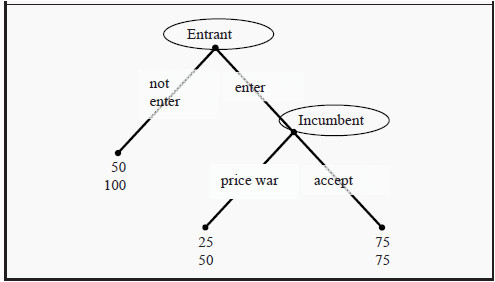
Figure 13.2: Game Tree
Finding the Nash Equilibrium for a Game Tree
To find the Nash Equilibrium for a game tree, we compare all different combinations of strategies. In the example in Section: Monopoly with No Barriers to Entry, E has two strategies and J has two. It is then possible to “translate” the game tree to a game on matrix form, as in Figure 13.3. Each strategy is translated into a row or a column. It now looks similar to the game from Section: The Prisoner’s Dilemma, but with other payoffs and strategies.
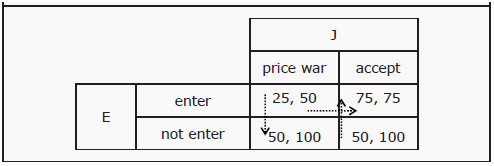
Figure 13.3: Payoff matrix for the Game Tree
Note that in the case when E chooses “not enter”, it does not matter what J chooses. Looking at the game tree in Figure 13.2, this is obvious since the game ends after such a choice and J never gets to choose. In the matrix, this translates into identical payoffs in all columns of the corresponding row, i.e.
(50, 100).
To find the Nash equilibrium, we use the same method as in the last section and check each square separately. E chooses in the vertical direction and J in the horizontal. In Figure 13.3, we have inserted arrows from squares that have a better alternative to that alternative. Squares that have no arrows going out will then be Nash equilibria. In this case, there are two Nash equilibria:
-
E chooses "enter" and J chooses "accept.” If E unilaterally changes her strategy, she will diminish her payoff from 75 to 50, and if J does so, she will diminish her payoff from 75 to 50.
-
E chooses “not enter” and J chooses “price war.” If E changes her strategy, she will diminish her payoff from 50 to 25, and if J does so, she will get the same as before, i.e. 100. The latter is due to the fact that it does not matter what J chooses when E has chosen “not enter.”
There is something odd with the latter Nash equilibrium. E chooses not to enter since J implicitly threatens with a price war. However, if E had established herself, J would have lost utility by actually starting a price war. According to the definition, this is a Nash equilibrium, but this objection leads us to introduce an alternative method of solving games on the extensive form.
Backward Induction
For game trees, such as the one in Section: Monopoly with No Barriers to Entry, there is another, often used, solution method. The main idea is to start at the end of the tree, and then solve it backward.
An example will make this clear. Consider the game tree in Figure 13.2 again. The last thing that happens in the game tree is that J chooses “price war” or “accept.” If she chooses the first option, she gets 50 and if she chooses the second, she gets 75. Obviously, it cannot be optimal to choose the first. Consequently,
given that E has chosen “enter,” J will choose “accept.” We can then reduce the game tree by omitting the alternative that J will not choose, and just keep the payoffs of the alternative that she does choose. The game tree will then look like in Figure 13.4.
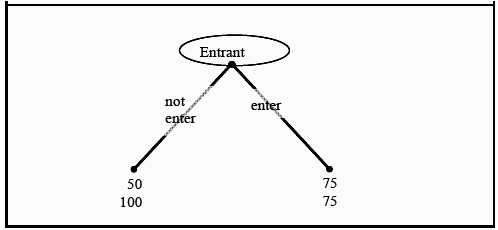
Figure 13.4: Reduced Game Tree
Given that J will choose “accept,” the choice for E is simpler. If she chooses “not enter” she will get 50 and if she chooses “enter” she will get 75. Consequently, she chooses the latter. The solution, using backward induction, is then
E: "enter"; J: "accept.”
Comparing this solution to the one in Section: Finding the Nash Equilibrium for a Game Tree (that had two different solutions, one of which is the same as the one here) this one seems more reasonable. Earlier, we found a Nash equilibrium in which E chose “not enter” and that included a (never realized) threat from J to start a price war.
Using backward induction, the threat reveals itself as being empty, and the only solution is that E establishes herself and J chooses to accept. The solution one obtains by using backward induction is called subgame perfect equilibrium.