Capital

If the firm rents its capital, the problem of how much to rent is, more or less, the same as the problem of how much labor to use. It rents precisely so much that the rental rate becomes equal to the marginal revenue product of capital (compare to Labor), i.e. until

MRPK = r ,

where r is the rental rate. In Production Costs , we used the rental rate to price capital. If instead the firm is to invest in capital, the problem is very different. The quantity of capital is not variable in the short run.

Often, the firm decides about investments that are to remain in place during many years and that are expected to generate future profits. It is therefore necessary to compare flows from different points in time with each other: Is it ok to spend a large sum today to get access to future profits of certain expected size and that would come scattered over several years. How should one deal with the risk that the future profits will be lower than expected?

Present Value

What does time mean for the value of a certain sum of money? Suppose that we want to know how much 100 (of any currency) that we will get one year from now is worth today. We could then reason like this: If it were possible to put 98 in a bank account at an interest rate of 2%, then in a year that would be worth 98*1.02 = 100.

Consequently, 100 in one year should be worth 98 today; the present value is 98. If we use that formula backwards, 100 in one year is worth 100/1.02 = 98 today, if the interest rate is 2 %. Similarly, 100 in two years is worth 100/(1.02)2 = 96 today, or more generally:

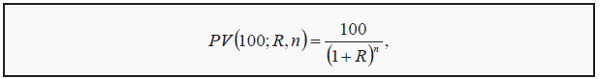
where PV(100,R,n) is the present value of 100, when the interest rate is R and the cash flow is in n years. If one knows which discount rate to use, it is easy to calculate the present value of future payments.

Bonds

We can use the present value formula to get the price of a bond. A bond is a security that gives the holder the right to a certain sum of money, the principal or face value, in a certain number of years. Often, the bond also pays a smaller amount each year, called the coupon. Some of the most important types of bonds are government bonds and corporate bonds.

Suppose we have a government bond that pays a coupon of 100 each year for ten years and then a face value of 1,000 in the tenth year. That means we will get ten payments. To calculate the present value of the future cash flows, we use the present value formula on each payment:

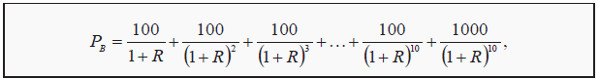
where PB is the price of the bond. If the discount rate is 2% as before, the bond would be worth 1 719.

Note, however, that bonds usually are not priced this way. Instead, the price is decided on the market; either in an auction or is negotiated between buyers and sellers. Then, one uses the formula to back out which discount rate is compatible with the price, the coupons, and the face value. It is usually impossible to find a formula to that. Instead, one uses a numerical method (that is often preprogrammed into calculators or spreadsheet programs) to find the correct discount rate.

Suppose that the ten year bond above does not cost 1 719, but is traded at a market price of 1,000. It is then possible to calculate that the discount rate is 10 %. In other words, if you use 0.10 instead of R in the formula above, the sum will be exactly 1,000. The discount rate one gets this way is called the yield to maturity, and can be viewed as an internal rate of return on the bond.

There is also an odd type of bonds called perpetual bonds, which have no end date. They pay a coupon each year forever. This type of bond is surprisingly easy to price. It is possible to show that the value of perpetual bond that pays 100 each year is

Conversely, if we know the price but not the yield: R = 100/P.

Stocks

Just as in the case of bonds, the price of stocks is usually set in the market. In principle though, one can use the present value formula to price them as well. As owner of a stock, one has the right to future dividends. With expectations of how large these will be, the present value of the future cash flows is:

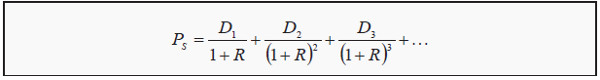
where PS is the price of the stock and Di is the expected dividend in year i. Unfortunately,

this formula is impossible to use since it contains an infinite number of terms and Di can vary between periods. However, if one is willing to assume that the dividends will grow at a constant growth rate, g, and that R is constant, it is possible to show that the formula can be simplified as (compare to the formula for a perpetual bond)

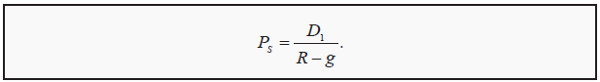
Note, however, that these assumptions are quite unrealistic. Dividend: A (usually yearly or quarterly) payment to the stockowners.

Correction for Risk

How do we get the correct discount rate? We have used R for all the discount rates above. However, interest rates for different securities differ substantially, and also change over time. The primary reason why, for instance, different bonds have different yields is that they have different levels of risk. A government bond is usually considered risk free whereas a corporate bond always has a risk that the issuer will not be able to fulfill her commitments.

Interest rates for mortgages vary with the risk that the borrower will not be able to pay interest or installments. Discount rates for stocks are not quoted, but if calculated they differ wildly depending on the underlying risk. The discount rate for a risky asset will consequently be higher than for a risk free asset (such as a government bond). Often, the higher discount rate is called a risk-corrected discount rate.

Diversifiable and Nondiversifiable Risk

Regarding risk, we must differentiate between diversifiable and nondiversifiable risk. Suppose you invest all your savings in stocks in only one firm. You are then exposed to the risk that this stock will rise or fall in value in an unpredictable way. That risk can be quite big. You can decrease the risk by instead investing in a mutual fund.

The part of the fund that is invested in a certain stock is still exposed to the risk in that stock. However, since a certain stock is only a small part of the fund, that risk is much smaller. Furthermore, other stocks might tend to move in the opposite way (they have negative correlation with each other), thereby offsetting some of the movements. That will reduce risk even more. You have now reduced the risk by diversifying your portfolio. All risk that you have discarded is diversifiable risk.

Correlation : A number between -1 and 1 that measures how two variables, such as the return on two stocks, tend to move in relation to each other.

Diversify : Invest in several different securities with different characteristics.

However, not all risk is diversifiable. To see that, imagine that you own all assets in the world. You would then have an enormous portfolio of stocks, bonds, currency, real estate, etc. You would still be exposed to some risk, though: The value of your portfolio would vary with the state of the world economy, for instance depending on the business cycle. The risk you are still exposed to is nondiversifiable (also called systematic risk or market risk).

If you own a portfolio that has the same composition as the world economy, i.e. has the same percentage stocks etc., you are also fully diversified and have no diversifiable risk at all. If you have any other composition in your risky portfolio (and you probably do), you are exposed to both diversifiable and nondiversifiable risk.

To have diversifiable risk is unnecessary and most of those who have a large fraction of diversifiable risk are probably not aware of the problem. It is easy to get rid of that risk, either by diversifying or by investing in a welldiversified fund. One can therefore not expect any risk premium for holding diversifiable risk in ones portfolio.

Remember that the risk premium (see: Certainty Equivalence and the Risk Premium ) is the sum one has to pay a risk-averse agent to assume a certain risk. Since there is no reason to pay anyone to assume a risk that is possible to do away with, there is no risk premium on diversifiable risk. Only nondiversifiable risk carries a risk premium. The risk premium is the main reason why stock owners in the long run have larger returns than, for instance, people who save only in savings accounts.

CAPM: Pricing Assets

Suppose we have a fund that invests in the world market portfolio described above. That fund will carry no diversifiable risk. It will then generate a certain expected return, RM (the market return). Part of that return is a compensation for risk. If one invests in the risk free rate, one gets a certain return of Rf.

Therefore, the market risk premium must be the difference between the two: RM - Rf. The risk premium is, consequently, the expected excess return one earns for assuming nondiversifiable risk.

We can use the market risk premium to price other securities. The most fundamental model for pricing financial assets is the CAPM (Capital Asset Pricing Model). It states that the risk premium on asset j is proportional to the risk premium on the whole market:

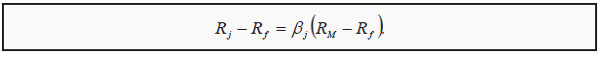
Here, Rj is the expected return on asset j; βj (beta) measures how asset j moves in relation to the market. If, for instance, asset j tends to rise 1 % when the market rises 1 %, βj = 1, whereas if it only tends to rise by 0.5 %, βj = 0.5. βj is then a measure of the riskiness of asset j, where only nondiversifiable risk is measured. The more nondiversifiable risk a certain asset has, the more it will covary with the market and the higher its β will be. Conversely, an asset with no nondiversifiable risk will have β = 0, so that Rj - Rf = 0. In other words, the discount rate is then equal to the risk free rate.

Pricing Business Projects

Often, CAPM is used to determine whether an investment is profitable or not. The idea is to first estimate how large the future profits will be. Thereafter one estimates how large the discount rate should be. Finally, one calculates the present value of the investment and determines if it is worth its cost or not.

We assume that we already have estimates of the future profits. We must then determine the riskiness of the project. That is often done by comparing it to other similar projects that already exist. If the new project cannot be considered either more or less risky than other projects in the firm, one can use the firm’s own internal rate of return as discount rate. However, suppose the firm is considering starting a new type of project.

It is then possible to get an estimate of the riskiness by studying other firms with similar projects. The new project should have about the same (nondiversifiable) risk. Therefore, we use the other firms to get an estimate of β. Then we use that estimate in the CAPM formula and solve for what the discount rate,Rj, should be: Rj = Rf + β( RM - Rf).

To give an example: Suppose we have a project that we expect will make a loss of 10 during the first year and then generate a profit of 200 during each of three consecutive years. Then we can sell the remains for 100. The present value of the future cash flows is

Furthermore, suppose that the market risk premium, RM - Rf, is 6 %, that the risk free rate of return, Rf, is 2 % and that β for a firm with a similar project is 1.5. We then estimate the discount rate to 2 % + 1.5*6 % = 11 %. If we use that value in the formula, the present value is 497.

Should we invest or not? That depends on the price. If the cost of the project is less than 497, we invest; if it is more, we do not. Often, one includes the cost in the present value. This is then called the net present value (NPV). The investment criterion is then whether NPV > 0 or not. Suppose the investment costs 450. Then NPV = -450 + 497 = 47, and we should go on with the investment since it is profitable.

Sometimes, one performs a slightly different analysis. With an estimate of the future cash flows and the investment cost, one can solve for the R that makes NPV equal to zero. (One would then use the same type of numerical procedure as for calculating the yield a bond.)

If the cost is still 450, R = 14.6 %. That rate is called the internal rate of return and can also be used as an investment criterion. If a project with the same risk (the same β) demands a return that is lower than 14.6 %, we invest, if it demands a higher return we do not.